Raypaths will be parameterized as a sum of a small number of Chebyshev polynomials. Fermat's principle allows us to optimize these raypaths with only group velocities, and not phase velocities. The coefficients of the raypaths can be saved in little computer memory.
In an anisotropic medium, traveltime tomography needs to construct raypaths from group velocities. A raypath traces the path of wave energy and by definition always parallels the energy-flow vector, or Poynting vector. (See standard texts on electromagnetic theory.) Let us identify the Poynting vector with the group velocity vector, whose more restrictive definition applies only to a narrow band of frequencies. When the high-frequency ray approximation is valid, we can calculate the traveltime of a wave between two points by integrating the group velocity along the ray between the points.
Most shooting methods of dynamic ray tracing require alternate use of both phase and group velocities. Using both velocities would be more inconvenient for traveltime tomography, which needs only group velocities to calculate traveltime from a valid raypath. A perturbation of group velocities would have to be reconciled with perturbations of phase velocities.
By contrast a relaxation method of ray tracing needs only the group velocity. A raypath designates a stationary path according to Fermat's principle: perturbing any portion of the path should increase the integrated traveltime. A relaxation method initializes the raypath with parameters that allow few degrees of freedom. The initial path should be stiff and unable to make any sudden changes in direction because early iterations will also have large errors in the reference velocity model. Some stiffness in a raypath is also necessary to model accurately the path of wave energy at finite frequencies. Parameters of the path are perturbed and adjusted until the integrated traveltime is minimized. Because errors in the path are reduced, the path is allowed more degrees of freedom, and the new parameters are perturbed and adjusted further. Optimization ends when no more detail in the raypath can be justified for a measurable sensitivity to the resulting perturbations of traveltime.
Describe a ray then as a sum of smooth basis functions. Prothero et al 1988 described raypaths as sums of sine functions and optimized these functions with a simplex search, which avoids the need to calculate Frechet derivatives. Berryman 1990 used a similar raypath optimization for crosswell applications. However, Frechet derivatives do allow faster convergence.
More recently Grechka and McMechan have used Chebyshev polynomials. I find that these polynomials optimize shorter traveltimes for diving waves from fixed surface points than do sums of sines and semicircles. Sines have much flatter derivatives at the endpoints and cannot begin at such a steep angle as the polynomials. A semicircle appears to encourage too steep an angle at the endpoints.
Chebyshev polynomials Tn(x) are defined
over the range ![]() by the recursion:
T0 (x) = 1,
T1 (x) = x, and
Tn+2 (x) = 2 x Tn+1 (x) - Tn (x).
As a minor modification, I prefer to shift the Chebyshev
polynomials so that endpoints are fixed, and coefficients
describe perturbations away from a straight line between
endpoints. Define functions Cn (x) over the range
by the recursion:
T0 (x) = 1,
T1 (x) = x, and
Tn+2 (x) = 2 x Tn+1 (x) - Tn (x).
As a minor modification, I prefer to shift the Chebyshev
polynomials so that endpoints are fixed, and coefficients
describe perturbations away from a straight line between
endpoints. Define functions Cn (x) over the range
![]() by
by
| |
||
| (6) |
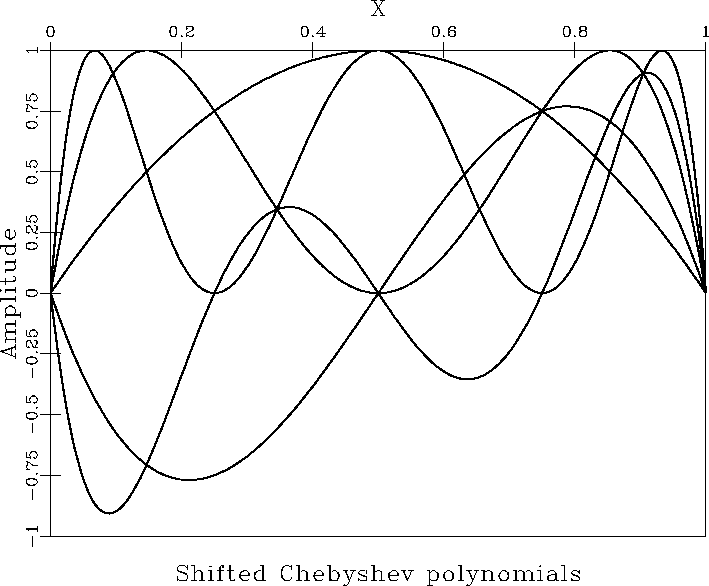
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the first 5 of these
shifted Chebyshev polynomials.
shows the first 5 of these
shifted Chebyshev polynomials.
 |
Let ![]() and
and ![]() be the Cartesian coordinates of the endpoints of the ray.
I assume that these points lie along a surface that is
roughly horizontal. Let
be the Cartesian coordinates of the endpoints of the ray.
I assume that these points lie along a surface that is
roughly horizontal. Let ![]() be the unit
vector pointing down the vertical axis of anisotropic symmetry.
I specify the location
be the unit
vector pointing down the vertical axis of anisotropic symmetry.
I specify the location ![]() along a raypath as a function of
the variable r, which ranges from 0 to 1 between the endpoints:
along a raypath as a function of
the variable r, which ranges from 0 to 1 between the endpoints:
![\begin{displaymath}
\vec{ \bf x}(r) = \vec{ \bf a} + r (\vec{ \bf b} - \vec{ \bf...
...]
[ \vec{ \bf \hat z} \times (\vec{ \bf b} - \vec{ \bf a}) ] .\end{displaymath}](img26.gif) |
(7) |
A small number of coefficients may be adequate to describe a 3D raypath. Such a raypath is much easier to store in memory than an ordered series of samples from the raypath. The stiffness of the raypath may also be controlled to describe more accurately the path of energy with finite bandwidth. Detailed complications of a raypath should be avoided on a scale finer than the spatial wavelengths being modeled.