As before, the signal ![]() is described by a
two-dimensional signal annihilation filter
is described by a
two-dimensional signal annihilation filter ![]() ,so that
,so that ![]() .The noise
.The noise ![]() is described by a noise annihilation filter
is described by a noise annihilation filter ![]() ,so that
,so that ![]() , where
, where
![]() is now a single two-dimensional filter.
As before, the recorded data
is now a single two-dimensional filter.
As before, the recorded data ![]() is the sum of the signal
is the sum of the signal ![]() and noise
and noise ![]() ,making
,making ![]() .
.
The use of filters to characterize the signal and noise
is similar to the methods used
to separate the signal and noise in the simple three-dip cases
shown in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Here, both the signal and noise are characterized by two-dimensional filters,
one filter for the noise and one filter for the signal.
Although the signal and noise in the three-dip case
considered in chapter
.
Here, both the signal and noise are characterized by two-dimensional filters,
one filter for the noise and one filter for the signal.
Although the signal and noise in the three-dip case
considered in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) did not overlap spatially,
in the general case the noise and signal will always overlap.
Because of this overlap,
calculating the signal filter
did not overlap spatially,
in the general case the noise and signal will always overlap.
Because of this overlap,
calculating the signal filter ![]() and the noise filter
and the noise filter ![]() may be
a problem, since the signal
may be
a problem, since the signal ![]() and noise
and noise ![]() are unavailable before
the separation takes place.
A combination of
two techniques is used to produce reasonable estimates of
are unavailable before
the separation takes place.
A combination of
two techniques is used to produce reasonable estimates of ![]() and
and ![]() here.
here.
The first technique is to separate spatially the noise and the signal into regions where one or the other dominates. For example, in the case of the ground-roll noise considered later in this section, the noise may be isolated to a narrow wedge within a shot gather. The noise filter calculated over the data in this wedge will be influenced primarily by the ground roll. A similar technique is used to calculate the signal filter. After the ground roll and the first breaks are muted, the data is dominated by the signal, so that a filter calculated over this data will be influenced primarily by signal.
The second technique used to produce reasonable estimates of ![]() and
and ![]() is to control the shape of the filters to produce the
desired prediction.
The signal filter
is to control the shape of the filters to produce the
desired prediction.
The signal filter ![]() is a purely lateral two-dimensional filter
as described in chapter
is a purely lateral two-dimensional filter
as described in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
If this filter is kept short in time,
the steeply dipping ground roll becomes fairly difficult to predict.
The noise filter
.
If this filter is kept short in time,
the steeply dipping ground roll becomes fairly difficult to predict.
The noise filter ![]() , on the other hand,
is shaped to follow the dip of the ground roll and has the form
, on the other hand,
is shaped to follow the dip of the ground roll and has the form
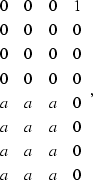 |
(136) |
Since this method will generally be used on prestack data,
either filter may be corrupted by high-amplitude noise.
Following the method presented in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
high-amplitude noise may be removed by a trace-to-trace prediction
method where samples that are not well predicted are thrown out.
These missing data samples, as well as data not recorded,
are then restored during the inversion for the signal and noise.
,
high-amplitude noise may be removed by a trace-to-trace prediction
method where samples that are not well predicted are thrown out.
These missing data samples, as well as data not recorded,
are then restored during the inversion for the signal and noise.
To review chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
the data
,
the data ![]() is separated into the known data
is separated into the known data ![]() and the missing data
and the missing data ![]() ,so that
,so that ![]() .Two masks,
.Two masks, ![]() and
and ![]() , are used to describe the missing data, making
, are used to describe the missing data, making
![]() and
and ![]() , where
, where ![]() , where
, where ![]() is the identity matrix.
is the identity matrix.
Summarizing the previous definitions:
![]() = data
= data
![]() = signal
= signal
![]() = noise
= noise
![]() = known data
= known data
![]() = missing data
= missing data
![]() = known data mask
= known data mask
![]() = missing data mask
= missing data mask
![]() = signal annihilation filter
= signal annihilation filter
![]() = noise annihilation filter.
= noise annihilation filter.
The relationships between these factors are as follows:
![]()
![]()
![]()
![]()
![]() or
or ![]() .
.
Taking ![]() and
and ![]() and replacing
and replacing ![]() with
with ![]() produces the system
produces the system
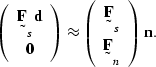 |
(137) |
Replacing the data ![]() with
with ![]() and moving the terms that depend
on the missing data
and moving the terms that depend
on the missing data ![]() to the right-hand side gives
to the right-hand side gives
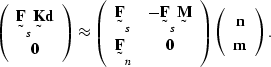 |
(138) |
Finally, system (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is modified
to weight the noise prediction
so that the noise tends to fall only in the zone where
the noise is expected.
In this case, the weighting is done by a simple set of weights,
) is modified
to weight the noise prediction
so that the noise tends to fall only in the zone where
the noise is expected.
In this case, the weighting is done by a simple set of weights,
![]() and
and ![]() ,
,
![]() being small where signal is expected and large where only
noise is expected,
and
being small where signal is expected and large where only
noise is expected,
and ![]() being small where noise is expected and large where only
signal is expected.
The modified system then becomes
being small where noise is expected and large where only
signal is expected.
The modified system then becomes
 |
(139) |
In the example shown here, the weight ![]() has been set to follow the
ground roll by a single velocity and a single window length.
An alternative approach that might
work well when the ground roll is very strong
would be to make
has been set to follow the
ground roll by a single velocity and a single window length.
An alternative approach that might
work well when the ground roll is very strong
would be to make ![]() the inverse of the envelope of the data.
This weighting function can also be used to describe the spatial
extent of the noise for calculating the noise and signal filters.
For signal and noise that vary as functions in time,
the two sets of weights can become functions such as the t and t2
in section
the inverse of the envelope of the data.
This weighting function can also be used to describe the spatial
extent of the noise for calculating the noise and signal filters.
For signal and noise that vary as functions in time,
the two sets of weights can become functions such as the t and t2
in section ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
To reduce the numbers of iterations required to solve
system (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
the initial estimate of
),
the initial estimate of ![]() is set to be the wedge of data dominated
by noise filtered by the signal annihilation filter
is set to be the wedge of data dominated
by noise filtered by the signal annihilation filter ![]() to remove
the signal that underlies the noise.
This estimate reduces the number of iterations and improves the
final estimate of
to remove
the signal that underlies the noise.
This estimate reduces the number of iterations and improves the
final estimate of ![]() significantly.
significantly.