Based on Green's second identity,
the integral expression for a pressure wavefield ![]() within a source free volume bounded by surface S is
within a source free volume bounded by surface S is
![]()
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
For seismic data, the integral can be split into two parts
so that S = S1 + S2 and the wavefield can be considered as arising
from causal sources below S1, which represents the data collection
surface. Since seismic data are recorded
for a finite time, the surface S2 can be chosen in such a way that
the contribution from this part of the integral is negligible.
The choice of Green's function that vanishes on surface S1 reduces
the integral to
).
For seismic data, the integral can be split into two parts
so that S = S1 + S2 and the wavefield can be considered as arising
from causal sources below S1, which represents the data collection
surface. Since seismic data are recorded
for a finite time, the surface S2 can be chosen in such a way that
the contribution from this part of the integral is negligible.
The choice of Green's function that vanishes on surface S1 reduces
the integral to
![]()
![]()
|
greensthm
Figure 1 Geometry for derivation of the Kirchhoff integral (after Berkhout, 1982). | 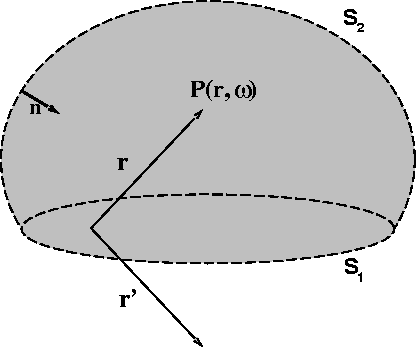 |
The surface integral then becomes
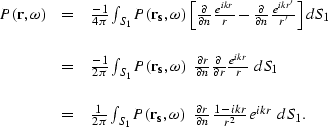
| |
(1) |
| |
(2) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) are the 3-D frequency and time
domain equations for the upward continuation of a scalar wavefield.
For computational efficiency it is common to make the far-field approximation
) are the 3-D frequency and time
domain equations for the upward continuation of a scalar wavefield.
For computational efficiency it is common to make the far-field approximation
If the wavefield is invariant in one space coordinate, the frequency domain equation can be rewritten as
![]()
| |
(3) |
| |
(4) |
| |
(5) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). His expression is similar
to equation (
). His expression is similar
to equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), except that his convolutional operator
depends on r. Berryhill's time domain formulation is accurate
since it includes the near-field term, but in practice, the added
computation of the delay-time variant convolution is often unnecessary.
), except that his convolutional operator
depends on r. Berryhill's time domain formulation is accurate
since it includes the near-field term, but in practice, the added
computation of the delay-time variant convolution is often unnecessary.
Equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) through (
) through (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) are the Kirchhoff
integral equations for upward
continuation. Wave-equation datuming is performed by implementing
these equations. Downward continuation is performed by means of the adjoint
processes. The concept of adjoint operators will be more fully described
in a subsequent section, but for now, it is only important to note that
the adjoint forms of the integral equations will have the opposite sign
in
) are the Kirchhoff
integral equations for upward
continuation. Wave-equation datuming is performed by implementing
these equations. Downward continuation is performed by means of the adjoint
processes. The concept of adjoint operators will be more fully described
in a subsequent section, but for now, it is only important to note that
the adjoint forms of the integral equations will have the opposite sign
in ![]() or in the time delay factor
or in the time delay factor ![]() .
The adjoint forms of the time domain integrals, along with the imaging
condition, result in Schneider's (1978) Kirchhoff migration operators.
Wiggins (1984) uses the far-field approximation in his implementation
of Kirchhoff datuming and migration.
.
The adjoint forms of the time domain integrals, along with the imaging
condition, result in Schneider's (1978) Kirchhoff migration operators.
Wiggins (1984) uses the far-field approximation in his implementation
of Kirchhoff datuming and migration.