Layer-stripping Kirchhoff as a semi-recursive method

The layer-stripping migration method can be thought of as a hybrid algorithm that incorporates some of the advantages of recursive migration with the efficiency of Kirchhoff migration. I call it semi-recursive because the depth step is much greater than that used in phase-shift or finite-difference shot-profile migrations. Because the data are re-synthesized at one or more depth levels in the subsurface, the method has the added advantage of implicitly handling multiple arrivals. In each datuming and imaging step the traveltime tables are single valued, but because the data are repropagated at every step, the final effect is equivalent to using multivalued traveltime tables.

This is illustrated by Figures  through , which compare recursive migration to standard Kirchhoff migration, and to the layer-stripping method. In a recursive method such as shot-profile migration, shots and geophones are downward continued through each depth level. Figure  illustrates this for one line of shots or geophones. It is evident that there are many propagation paths from the surface to the image point; therefore, multiple arrivals are handled. The computation is performed for all frequencies.

By contrast, first-arrival Kirchhoff migration is performed by summing data over trajectories defined by the propagation paths illustrated in Figure . There is only one path linking each surface position to the image point; therefore, multiple arrivals are not handled. Although crossing paths are not illustrated here, they can occur.

The layer-stripping method is illustrated in Figure . It is a combination of Kirchhoff wave-equation datuming and Kirchhoff migration. There are multiple propagation paths from the surface to the image point; therefore, multiple arrivals are handled. The computation is illustrated for the Marmousi model in Figure  and proceeds as follows:

1.

Calculation of traveltimes from the surface (Figure a). These traveltimes are used to:

• Migrate from the surface to some depth level z₁ or lower.
• Downward continue to depth level z₁ (Figure b).

2.

Calculation of traveltimes from depth level z₁ (Figure c). These traveltimes are used to:

• Migrate from depth level z₁ (Figure d).

The depth step of Kirchhoff downward continuation is much larger than the $\triangle z$ used in shot-profile migration. Since there are multiple paths from the surface to the image point, multiple arrivals are handled. Because the paths are shorter than in Figure , first-arrival traveltimes are more likely to be valid.

 

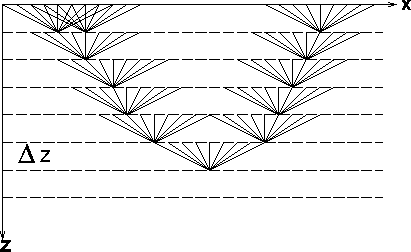
s-g Figure 8 Propagation paths for shot-profile migration. A few representative propagation paths from the surface to an image point for shot-profile migration. There are many paths from each surface location to the depth point.

 

kirch Figure 9 Propagation paths from the surface to an image point for Kirchhoff migration. There is only one path from each surface location to the depth point.

 

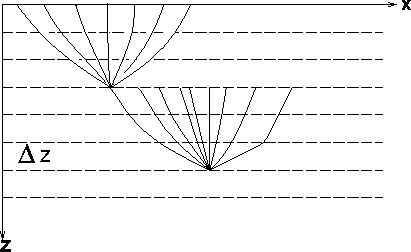
datum Figure 10 Propagation paths from the surface to a depth point for layer-stripping Kirchhoff downward continuation and migration. Paths traverse shorter distances so they are less likely to cross, and there are multiple paths to each depth point.

 

calc
Figure 11 Illustration of layer-stripping Kirchhoff datuming and migration. The velocity model is divided into two parts. (a) Finite-difference traveltimes are calculated in the upper part of the model. (b) These traveltimes are used to image the upper portion of the data and downward continue the wavefield, resynthesizing it at depth level z₁. (c) Traveltimes are calculated from depth level z₁ and (d) used to image the downward continued wavefield. Movie.