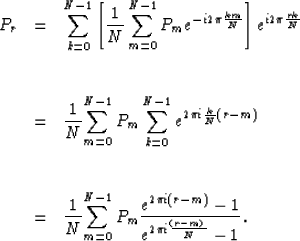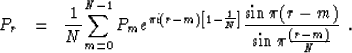Next: REFERENCES
Up: INTRODUCTION
Previous: Interpolation in Stolt migration
The slow Fourier transform of an evenly sampled signal in time
can be written as
| 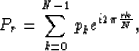 |
(10) |
where the index k is an integer corresponding to the evenly sampled
time values, while the variable r is a real number:
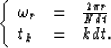
In equation (9), we take the slow Fourier transform of
the inverse fast Fourier transform. Introducing the inverse FFT inside
equation (10) we have
| 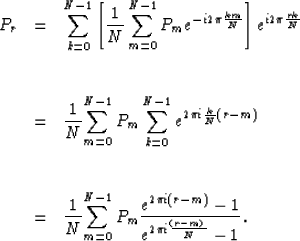 |
(11) |
The expression inside the sum provides a formula for a new interpolation
method
| 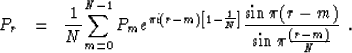 |
(12) |
Observe that for 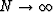 the interpolator becomes
identical to the one presented by Rosenbaum and Boudreaux (1981):
the interpolator becomes
identical to the one presented by Rosenbaum and Boudreaux (1981):
| 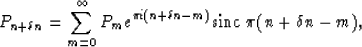 |
(13) |
where we replaced r by  . A truncated version of the
Rosenbaum interpolation formula is used by Harlan (1982), showing
better artifact reduction than any other classic interpolation method.
The interpolation formula in equation (12) is shown
to produce even better results then those found by Harlan (Lin et al., 1993).
. A truncated version of the
Rosenbaum interpolation formula is used by Harlan (1982), showing
better artifact reduction than any other classic interpolation method.
The interpolation formula in equation (12) is shown
to produce even better results then those found by Harlan (Lin et al., 1993).





Next: REFERENCES
Up: INTRODUCTION
Previous: Interpolation in Stolt migration
Stanford Exploration Project
11/16/1997
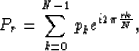
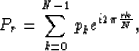
![]()