Next: CONCLUSIONS
Up: EXAMPLES
Previous: Lowpass Filter
The wavefield extrapolator in three dimensions is
given by Equation 8. The extrapolator for a given temporal
frequency 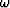 is a circularly symmetric operator in (kx - ky) domain.
is a circularly symmetric operator in (kx - ky) domain.
| ![\begin{displaymath}
D(k_x,k_y)= \exp{\left \{ i\frac{\Delta{z}}{\Delta{x}}\left[...
...lta x}{v}}^2 \right )
-k_x^2 - k_y^2 \right]^{1/2} \right \}},\end{displaymath}](img19.gif) |
(8) |
where v is the velocity while kx and ky are the normalized
wavenumbers such that any distance quantity is measured in
terms of the horizontal sampling
interval 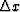 . Throughout this paper k refers to the normalized
wavenumber.
extrap3d
. Throughout this paper k refers to the normalized
wavenumber.
extrap3d
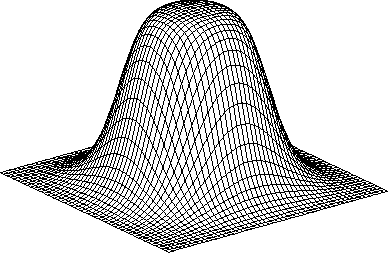
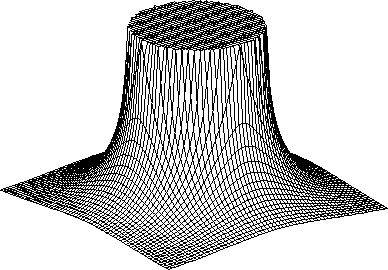
Figure 7 Ideal 3-D extrapolator in the wavenumber (kx-ky) domain for a
particular temporal frequency 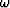 . The circular region in the
center is the propagating region and the region external to it is
the evanescent region.
The two horizontal axes are the normalized
wavenumbers kx and ky and they go from -0.5 to 0.5 cycles/s.
. The circular region in the
center is the propagating region and the region external to it is
the evanescent region.
The two horizontal axes are the normalized
wavenumbers kx and ky and they go from -0.5 to 0.5 cycles/s.





The circular symmetry of the operator enables
it to be realized using McClellan filter.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the ideal-extrapolator in 3-D for a certain
temporal frequency
shows the ideal-extrapolator in 3-D for a certain
temporal frequency 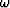 . The parameters used in generating
the extrapolator
are dx=dz=12.5 m,
. The parameters used in generating
the extrapolator
are dx=dz=12.5 m, 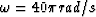 , and v = 1000. m/s.
A tapered 1-D extrapolator was designed by applying a
Gaussian taper to the ideal explicit wavefield extrapolation filter.
This leads to a stable extrapolation filter as described in Nautiyal et al, 1993.
The Gaussian taper is given by
, and v = 1000. m/s.
A tapered 1-D extrapolator was designed by applying a
Gaussian taper to the ideal explicit wavefield extrapolation filter.
This leads to a stable extrapolation filter as described in Nautiyal et al, 1993.
The Gaussian taper is given by 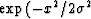 )
where
)
where  is a parameter to
be chosen.
Figure
is a parameter to
be chosen.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the amplitude spectrum for the ideal and
the tapered extrapolator . The extrapolation filter in two dimensions is
a symmetric filter with complex coefficients. Figure
shows the amplitude spectrum for the ideal and
the tapered extrapolator . The extrapolation filter in two dimensions is
a symmetric filter with complex coefficients. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the absolute
magnitude of the filter coefficients. Using the filter coefficients for
the tapered extrapolator, I generated the corresponding 3-D extrapolator
(Figure
shows the absolute
magnitude of the filter coefficients. Using the filter coefficients for
the tapered extrapolator, I generated the corresponding 3-D extrapolator
(Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) at
the frequency
) at
the frequency 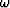 using the McClellan transformation. Compare this
3-D extrapolator with the ideal one shown in Figure
using the McClellan transformation. Compare this
3-D extrapolator with the ideal one shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
explicit
Figure 8 The ideal 2-D wavefield extrapolator (continuous curve) and
the tapered extrapolator (dashed curve) in wavenumber domain.
|
|  |
migfil
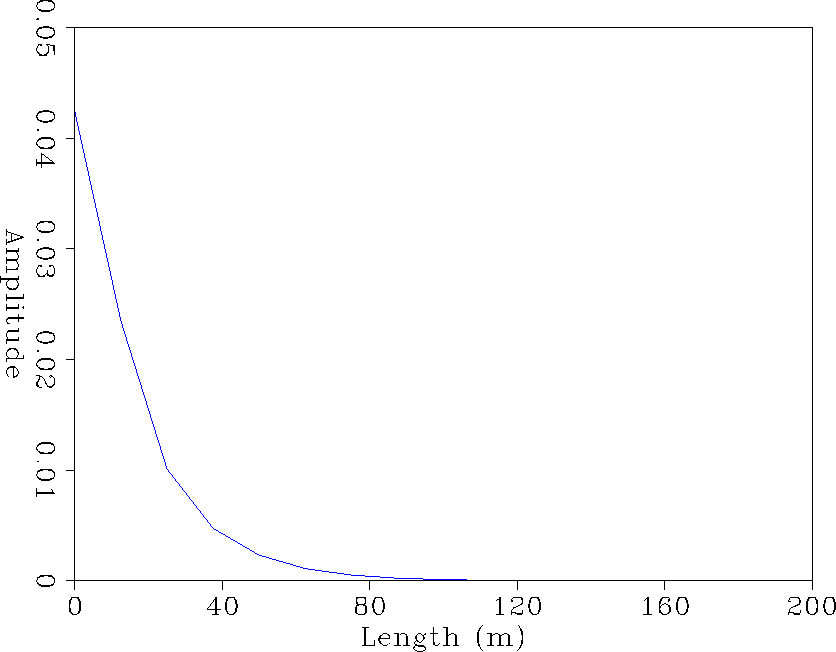
Figure 9 The magnitude of the tapered extrapolator in space domain. The filter
coefficients are complex. It is a nineteen coefficient symmetric operator.
The spatial wavelet magnitude is shown for one side.
|
|  |




 mclextrap3d
mclextrap3d
Figure 10 3-D wavefield extrapolator in (kx-ky) domain
generated using McClellan transformation.
Compare the operator to the ideal operator in Figure 7.










Next: CONCLUSIONS
Up: EXAMPLES
Previous: Lowpass Filter
Stanford Exploration Project
11/17/1997
![\begin{displaymath}
D(k_x,k_y)= \exp{\left \{ i\frac{\Delta{z}}{\Delta{x}}\left[...
...lta x}{v}}^2 \right )
-k_x^2 - k_y^2 \right]^{1/2} \right \}},\end{displaymath}](img19.gif)
![\begin{displaymath}
D(k_x,k_y)= \exp{\left \{ i\frac{\Delta{z}}{\Delta{x}}\left[...
...lta x}{v}}^2 \right )
-k_x^2 - k_y^2 \right]^{1/2} \right \}},\end{displaymath}](img19.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the ideal-extrapolator in 3-D for a certain
temporal frequency
shows the ideal-extrapolator in 3-D for a certain
temporal frequency ![]() . The parameters used in generating
the extrapolator
are dx=dz=12.5 m,
. The parameters used in generating
the extrapolator
are dx=dz=12.5 m, ![]() , and v = 1000. m/s.
A tapered 1-D extrapolator was designed by applying a
Gaussian taper to the ideal explicit wavefield extrapolation filter.
This leads to a stable extrapolation filter as described in Nautiyal et al, 1993.
The Gaussian taper is given by
, and v = 1000. m/s.
A tapered 1-D extrapolator was designed by applying a
Gaussian taper to the ideal explicit wavefield extrapolation filter.
This leads to a stable extrapolation filter as described in Nautiyal et al, 1993.
The Gaussian taper is given by ![]() )
where
)
where ![]() is a parameter to
be chosen.
Figure
is a parameter to
be chosen.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the amplitude spectrum for the ideal and
the tapered extrapolator . The extrapolation filter in two dimensions is
a symmetric filter with complex coefficients. Figure
shows the amplitude spectrum for the ideal and
the tapered extrapolator . The extrapolation filter in two dimensions is
a symmetric filter with complex coefficients. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the absolute
magnitude of the filter coefficients. Using the filter coefficients for
the tapered extrapolator, I generated the corresponding 3-D extrapolator
(Figure
shows the absolute
magnitude of the filter coefficients. Using the filter coefficients for
the tapered extrapolator, I generated the corresponding 3-D extrapolator
(Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) at
the frequency
) at
the frequency ![]() using the McClellan transformation. Compare this
3-D extrapolator with the ideal one shown in Figure
using the McClellan transformation. Compare this
3-D extrapolator with the ideal one shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.