




Next: Wave-equation Datuming for laterally
Up: WAVE-EQUATION DATUMING ALGORITHM
Previous: WAVE-EQUATION DATUMING ALGORITHM
We can epitomize the datuming algorithm in a depth
varying velocity by writing the successive operators
in matrix form. For simplicity I will take only
a datum with three depth levels
similar to the one in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The algorithm can be generalized for any number of
depth levels and any datum geometry.
For each value of
.
The algorithm can be generalized for any number of
depth levels and any datum geometry.
For each value of 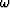 we have
we have
| ![\begin{displaymath}
\displaystyle{
\left[
\begin{array}
{ccc}
A&B&C
\end{arra...
...
\left[
\begin{array}
{c}
P(x,z=0,{\omega})\end{array}\right]
}\end{displaymath}](img13.gif) |
(6) |
where 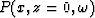 represents the zero-offset data after
Fourier transformation along the time axis.
The matrix
represents the zero-offset data after
Fourier transformation along the time axis.
The matrix
![\begin{displaymath}
\left[
\begin{array}
{c}
FT \\ \end{array}\right]\end{displaymath}](img14.gif)
performs the Fourier Transform matrix of the horizontal space variable.
Therefore the matrix
![\begin{displaymath}
\left[
\begin{array}
{ccc}
FT^* & & \\ &FT^* & \\ & &FT^* \\ \end{array}\right]\end{displaymath}](img15.gif)
is composed of inverse Fourier Transform block matrices, each being
the conjugate transpose to the direct transformation.
The matrix
![\begin{displaymath}
\left[
\begin{array}
{c}
W_1\\ W_2 W_1\\ W_3 W_2 W_1\\ \end{array}\right]\end{displaymath}](img16.gif)
contains three blocks corresponding to the
product of diagonal matrices of the form
| ![\begin{displaymath}
W_i=
\left[
\begin{array}
{cccccc}
e^{ik_{zi1} \Delta z} &...
...& & \\ & & & & &e^{ik_{zi6} \Delta z} \\ \end{array}\right] .\end{displaymath}](img17.gif) |
(7) |
On each diagonal are the phase-shifting exponentials
necessary to upward extrapolate the wavefield to a depth level.
The value of (kz)ij is given by the dispersion relation:
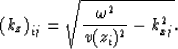
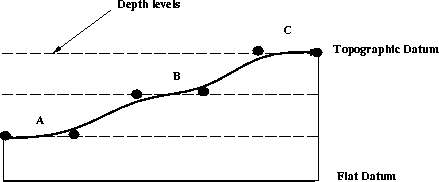
Datumatrix
Figure 2 Datuming for only three depth levels. Data extrapolated to the
first depth level is extracted by matrix A, to the second
level by matrix B and to the third by matrix C.
|
|  |

The matrices A,B,C are matrices corresponding
to the shape of the datum.
For the case shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) the matrices A,B,C are
the matrices A,B,C are
![\begin{displaymath}
A=
\left[
\begin{array}
{cccccc}
1& & & & & \\ &1& & & & \\...
... & & &.& & \\ & & & &1& \\ & & & & &1 \\ \end{array}.
\right]\end{displaymath}](img19.gif)
The conjugate transpose algorithm can be obtained by reversing
the order of matrix multiplication in equation (6)
and transposing-conjugating each matrix. The matrices
A,B,C are diagonal matrices and therefore equal to the
transpose.
For each value of the frequency 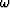 the conjugate datuming is
the conjugate datuming is
| ![\begin{displaymath}
\displaystyle{
\left[
\begin{array}
{c}
FT^* \\ \end{arra...
...ft[
\begin{array}
{c}
P(x,z_{dat},{\omega})\end{array}\right]
}\end{displaymath}](img20.gif) |
(8) |
where 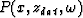 represents the wavefield recorded on
the topographic datum. The matrices W*i are conjugate transposed
of the diagonal matrices Wi which are explicitly represented in
equation (7).
represents the wavefield recorded on
the topographic datum. The matrices W*i are conjugate transposed
of the diagonal matrices Wi which are explicitly represented in
equation (7).





Next: Wave-equation Datuming for laterally
Up: WAVE-EQUATION DATUMING ALGORITHM
Previous: WAVE-EQUATION DATUMING ALGORITHM
Stanford Exploration Project
11/17/1997
![\begin{displaymath}
\displaystyle{
\left[
\begin{array}
{ccc}
A&B&C
\end{arra...
...
\left[
\begin{array}
{c}
P(x,z=0,{\omega})\end{array}\right]
}\end{displaymath}](img13.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The algorithm can be generalized for any number of
depth levels and any datum geometry.
For each value of
.
The algorithm can be generalized for any number of
depth levels and any datum geometry.
For each value of ![\begin{displaymath}
\displaystyle{
\left[
\begin{array}
{ccc}
A&B&C
\end{arra...
...
\left[
\begin{array}
{c}
P(x,z=0,{\omega})\end{array}\right]
}\end{displaymath}](img13.gif)
![]()
![\begin{displaymath}
\left[
\begin{array}
{ccc}
FT^* & & \\ &FT^* & \\ & &FT^* \\ \end{array}\right]\end{displaymath}](img15.gif)
![\begin{displaymath}
\left[
\begin{array}
{c}
W_1\\ W_2 W_1\\ W_3 W_2 W_1\\ \end{array}\right]\end{displaymath}](img16.gif)
![\begin{displaymath}
W_i=
\left[
\begin{array}
{cccccc}
e^{ik_{zi1} \Delta z} &...
...& & \\ & & & & &e^{ik_{zi6} \Delta z} \\ \end{array}\right] .\end{displaymath}](img17.gif)
![]()

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) the matrices A,B,C are
the matrices A,B,C are
![\begin{displaymath}
A=
\left[
\begin{array}
{cccccc}
1& & & & & \\ &1& & & & \\...
... & & &.& & \\ & & & &1& \\ & & & & &1 \\ \end{array}.
\right]\end{displaymath}](img19.gif)
![]() the conjugate datuming is
the conjugate datuming is
![\begin{displaymath}
\displaystyle{
\left[
\begin{array}
{c}
FT^* \\ \end{arra...
...ft[
\begin{array}
{c}
P(x,z_{dat},{\omega})\end{array}\right]
}\end{displaymath}](img20.gif)