




Next: Two conjugate transpose datuming
Up: Popovici : v(x,z) datuming
Previous: Introduction
Wave-equation datuming is the 2-D equivalent of the 1-D static shifting.
It takes seismic data from a given surface and transports it
to another surface. We hope that in the transportation process
nothing is lost, and seismic data will look exactly as if it
is recorded on the secondary surface.
We can formulate the datuming algorithm in a similar way
we can formulate the migration algorithm being the conjugate transpose of
the modeling algorithm. Given the data recorded on a
non-level surface, we want to continue the data to
a level surface. We can define the direct problem as
a wave equation extrapolation from a level surface to
an irregular surface. The conjugate transpose to this
problem will bring the data from the irregular topographic
surface to the level surface.
The direct problem is easier to formulate than the conjugate.
Suppose we record
a wavefield in a zero-offset experiment on a flat surface. The direct
problem is to upward continue the wavefield to the uneven surface,
similar to the one in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
I propose a scheme in which the wavefield is propagated upward
using a phase-shift or PSPI method and the values of the wavefield
are extracted at each height corresponding to the datum.
The advantage of the method is that it allows us to use
simple and fast algorithms to extrapolate the wavefield while
the disadvantage is that the algorithm is only an approximation to the exact solution.
.
I propose a scheme in which the wavefield is propagated upward
using a phase-shift or PSPI method and the values of the wavefield
are extracted at each height corresponding to the datum.
The advantage of the method is that it allows us to use
simple and fast algorithms to extrapolate the wavefield while
the disadvantage is that the algorithm is only an approximation to the exact solution.
Datumdraw
Figure 1 Data recorded on the flat datum (1) is extrapolated to the datum (2)
and then, using the conjugate transpose algorithm it is extrapolated back
to the flat datum(3).
|
| 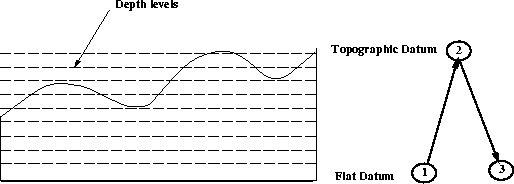 |

The conjugate transpose algorithm starts
by downward extrapolating the data from the highest point
on the topographic datum. Each time the wavefield reaches
the datum, data is inserted into the downward propagated wavefield.
The mathematical formulation of the direct datuming algorithm
is simpler in the case of depth variable velocity.
However I should note that for computational purposes there
is almost no speed difference between a depth varying
velocity v(z) medium and a laterally and depth
varying velocity v(x,z) medium.
The wavefield p(x,z=0,t) is Fourier transformed in time
to have 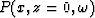 and each frequency can be independently
upward extrapolated. By Fourier transforming the horizontal space variable,
the wave equation can be written as
and each frequency can be independently
upward extrapolated. By Fourier transforming the horizontal space variable,
the wave equation can be written as
| 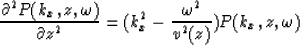 |
(1) |
valid for all values of kx and 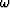 .For a constant velocity medium we introduce a constant kz as
.For a constant velocity medium we introduce a constant kz as
| ![\begin{displaymath}
k_z={\pm {[{\omega^2 \over v^2}-{k^2_x }]^{1 \over 2}}}.\end{displaymath}](img4.gif) |
(2) |
kz is constant for two given values of kx and 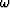 .Equation (1) becomes an ordinary differential equation
.Equation (1) becomes an ordinary differential equation
| 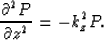 |
(3) |
For a constant kz it has the analytic solution
| 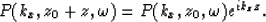 |
(4) |
For depth varying velocity v(z), kz is considered
approximately constant for small depth intervals (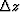 )
where the velocity is considered constant.
Therefore equation (4) can be written
)
where the velocity is considered constant.
Therefore equation (4) can be written
| 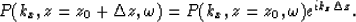 |
(5) |
This form of the equation can be used to downward or upward extrapolate
the wavefield for a small depth interval.
Thus the forward datuming algorithm can be summarized in four steps.
- Fourier transform the wavefield
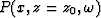 over the space
variable x.
over the space
variable x.
- Upward propagate the wavefield
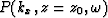 to the
next depth level
to the
next depth level 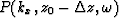 .
. - Forward transform the wavefield
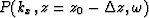 over the space variable x
over the space variable x
- Extract the traces corresponding to a depth level on
the topographic surface.





Next: Two conjugate transpose datuming
Up: Popovici : v(x,z) datuming
Previous: Introduction
Stanford Exploration Project
11/17/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
I propose a scheme in which the wavefield is propagated upward
using a phase-shift or PSPI method and the values of the wavefield
are extracted at each height corresponding to the datum.
The advantage of the method is that it allows us to use
simple and fast algorithms to extrapolate the wavefield while
the disadvantage is that the algorithm is only an approximation to the exact solution.
.
I propose a scheme in which the wavefield is propagated upward
using a phase-shift or PSPI method and the values of the wavefield
are extracted at each height corresponding to the datum.
The advantage of the method is that it allows us to use
simple and fast algorithms to extrapolate the wavefield while
the disadvantage is that the algorithm is only an approximation to the exact solution.
