Interpolation by wavelets

As in Fourier space, padding zeroes to the detail end of the wavelet vector interpolates the time series after transforming the vector back to the time domain. In contrast to interpolation in the Fourier domain, the base functions of the wavelet transform are local, and the extended spectrum contains small but noticeable energy as seen in Figure 6. In the case of a Haar transform, we would implement a next neighbour interpolation.

 

opol
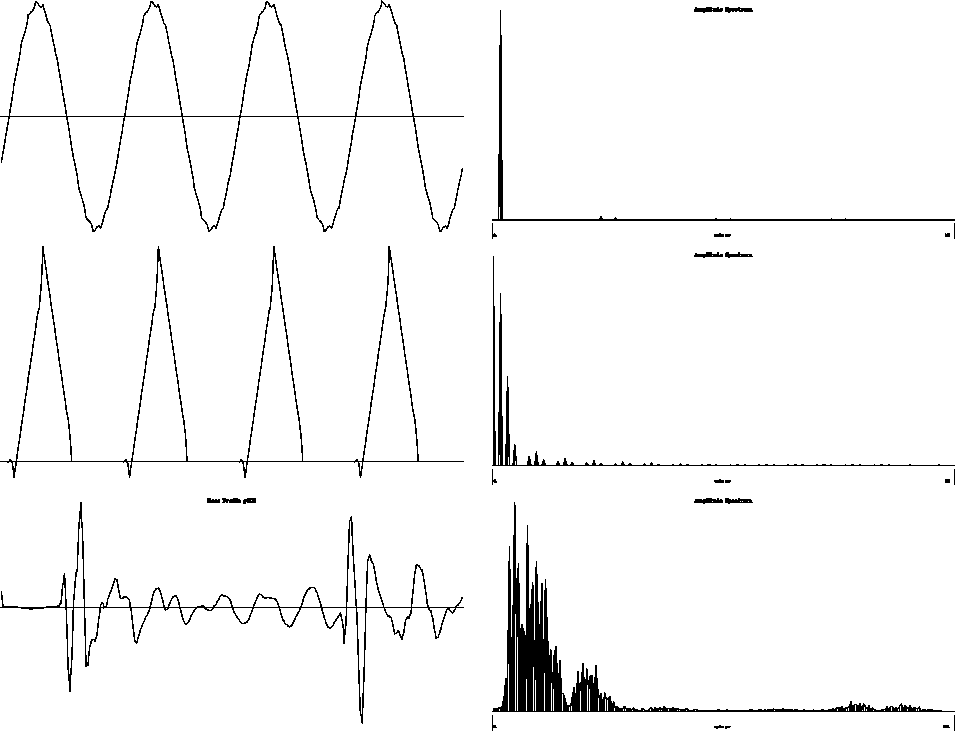
Figure 5 The original test functions and their spectra. The result of interpolating these functions is displayed in Figure 6.

 

ipol
Figure 6 Interpolation by discrete wavelet transformation. Traces of 256 samples are oversampled by transforming them into the wavelet domain, padding 256 zeroes at the high-frequency end, and inverse transforming them. The triangle and sinusoid series are distorted. The spikiness in time may be realistic in the trace example. Most, but not all, of the high-frequency energy is caused by the transforms wraparound feature. The characteristics of this interpolation scheme remain to be studied.