Data compression

The objective of data compression is to store information efficiently. Some conservative data compression schemes achieve this compression without changing the input data. Other approaches reduce the data down to their essential features and store only those features. Obviously, for such a compression to be successful, the correct reduction or filter step must be used. The correct filter preserves the data features which we consider essential.

Data compression by wavelet transformation is accomplished by storing the location of the significant samples and omitting the insignificant values. In practice a hybrid method is often used. The values and location of the maximum samples are stored. Intermediate sized sample values are stored by one- or two-bit representation of their value. Sample values below a certain threshold are neglected. In this project I did not store the actual sample values, because I was primarily interested in the effects of filtering in the wavelet domain.

In wavelet compression the input data are transformed and small sample values are neglected. In Figures 7 and 8, I have erased all samples smaller than 10 % of the maximum value. This leaves only about 8 % of the samples as nonzero.

The purpose of a video telephone picture of a person is to be recognizable. Little details are often negligible. The reduction step can be tested by interviewing users about their satisfaction. However, for seismic data it is hard to decide which details might be of importance in latter interpretation. Without a clear definition of what we want to preserve, a data compression by reduction cannot finally be evaluated.

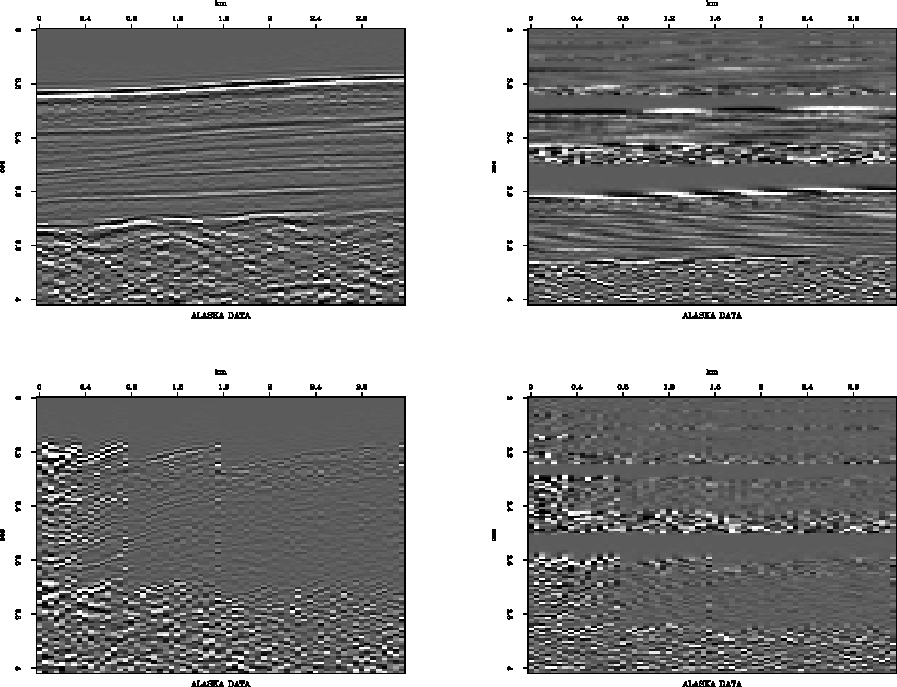
Data which depict a sparse wavelet transform are suited for compression by DWT. In Figure 7 the photograph's wide, smooth areas like the forehead and the cheeks are bounded by edges such as the hair line or the facial oval. The data yield a fairly sparse wavelet transform. Only few detail coefficients corresponding to the edges are of substantial size. Unfortunately, seismic data do not yield such a sparse matrix. Zeroing values below the 10 % threshold leaves the data severely distorted as seen in Figure 8. Seismic velocity spectra or well logs might be more suitable for compression by wavelet transformation.

 

plane2
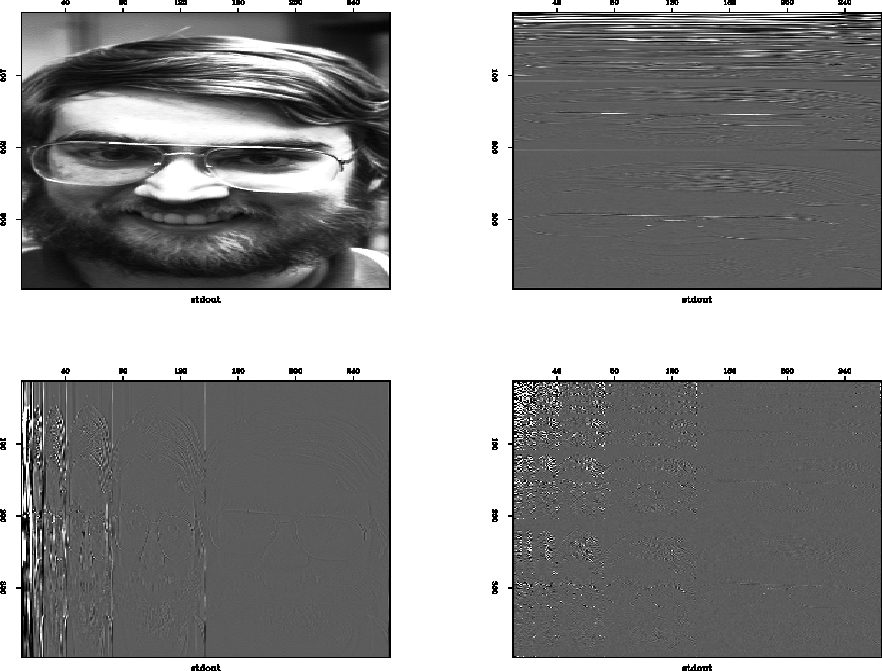
Figure 7 Two-dimensional wavelet transform of a picture. The input picture (top left) is transformed in the vertical (top right) and horizontal (bottom left) directions. Note that the face is repeated in the different octave subspaces of all transformed matrices. The lower right quarter of the matrix shows the edge details of the face. The glasses are depicted differently in each of the outer quarters of the matrix. These quarters, as well as the horizontally and vertically transformed matrix, are biased toward the horizontal and vertical edges, respectively. Unfortunately, these details are hardly visible in the paper document.

 

plane1
Figure 8 Two-dimensional wavelet transform of a seismic section. The same sequence of wavelet transformation as Figure 7, except that the data object is a seismic section.

 

comp
Figure 9 Data compression by wavelet transform. The 2-D transformation of the previous examples of Figure 7 and 8 is used for data reduction. In the wavelet domain every sample value smaller than a certain threshold (10 % maximum value) is erased. The top panels depict the reduced wavelet coefficient matrices. The middle panels show the reconstructed picture. The bottom row shows the difference between the inverted sections and the original data. In the electronic version of this book pushing the button let you explore data compression by wavelet transformation interactively.