




Next: CONCLUSION
Up: Ji: LS imaging, datuming
Previous: LEAST-SQUARES DATUMING
The forward modeling for sparsely sampled data
can be formulated by applying a subsampling operator to
the exploding reflector modeling operator as follows:
| 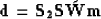 |
(8) |
where data 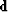 and image
and image 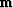 have different lengths
in the space direction because of the subsampling operator
have different lengths
in the space direction because of the subsampling operator 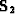 ,and the exploding reflector modeling operator
,and the exploding reflector modeling operator 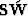 ,the same operator as equation (2),
can be any modeling operator such as Kirchhoff,
phase-shift, or finite-difference.
For a given sparsely sampled wavefield, we can estimate
a dense image by minimizing the error between the given wavefield
and the wavefield modeled by the modeling equation(7),
which is as follows:
,the same operator as equation (2),
can be any modeling operator such as Kirchhoff,
phase-shift, or finite-difference.
For a given sparsely sampled wavefield, we can estimate
a dense image by minimizing the error between the given wavefield
and the wavefield modeled by the modeling equation(7),
which is as follows:
| 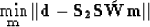 |
(9) |
Experiments were done using the Kirchhoff and phase-shift operators.
For a simple syncline reflector shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (a),
a synthetic model was generated using the Kirchhoff modeling operator
and the subsampled by zapping every other trace.
The result of modeling is shown in Figure
(a),
a synthetic model was generated using the Kirchhoff modeling operator
and the subsampled by zapping every other trace.
The result of modeling is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (b).
By applying the conjugate operator,
(b).
By applying the conjugate operator, 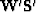 , to the subsampled
data, we get an interpolated image, as shown in Figure
, to the subsampled
data, we get an interpolated image, as shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (c).
It is very difficult to distinguish the effect of
the subsampling operator from the artifacts of the Kirchhoff
operator, but we can see that this image is very similar to the image
obtained without the subsampling operator shown in Figure
(c).
It is very difficult to distinguish the effect of
the subsampling operator from the artifacts of the Kirchhoff
operator, but we can see that this image is very similar to the image
obtained without the subsampling operator shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (c).
The image obtained by the least-squares interpolation is shown
in Figure
(c).
The image obtained by the least-squares interpolation is shown
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (d); it closely resembles the image
obtained from the data without subsampling.
(d); it closely resembles the image
obtained from the data without subsampling.
Another experiment done using the Gazdag operator
is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
This result also closely resembles that for the images
without subsampling.
The reason may be that the wavefront healing effect during
the extrapolation.
.
This result also closely resembles that for the images
without subsampling.
The reason may be that the wavefront healing effect during
the extrapolation.
Kirint
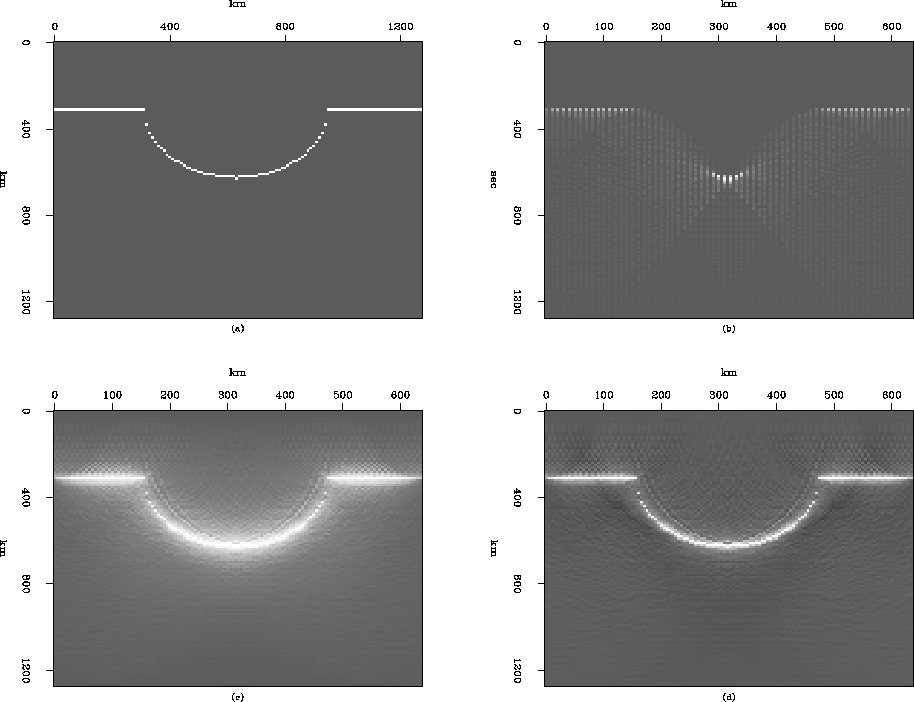
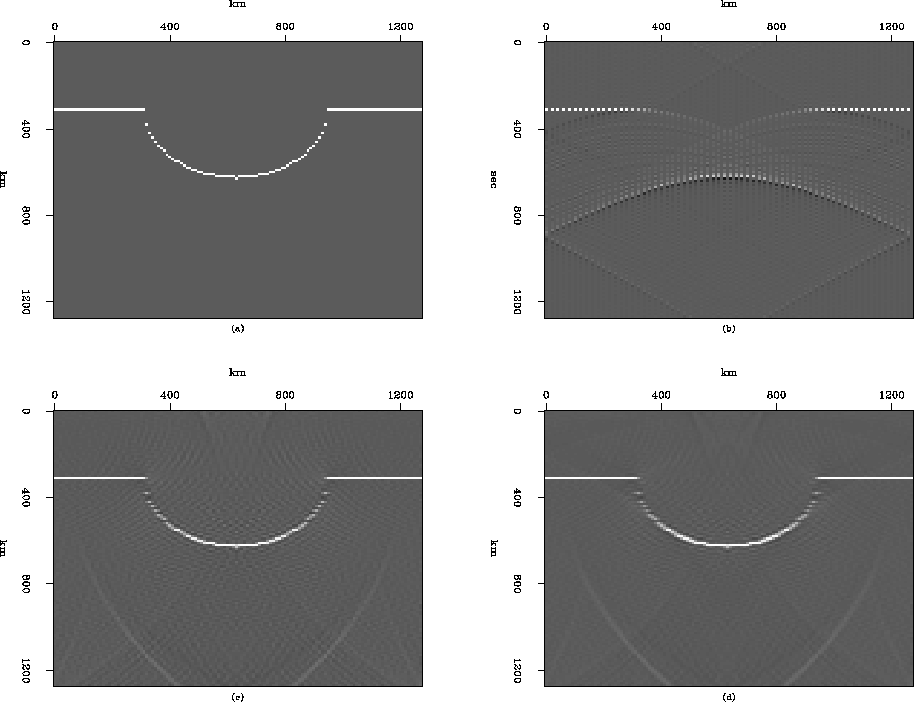
Figure 10 Least-squares Kirchhoff interpolation:
(a) The original image used to generate the subsampled
wavefield shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (b),
(b) The subsampled wavefield.
(c) The interpolated subsurface image obtained
by Kirchhoff migration with a subsampling operator,
(d) The interpolated subsurface image obtained
by least-squares Kirchhoff interpolation
(after 10 iterations).
(b),
(b) The subsampled wavefield.
(c) The interpolated subsurface image obtained
by Kirchhoff migration with a subsampling operator,
(d) The interpolated subsurface image obtained
by least-squares Kirchhoff interpolation
(after 10 iterations).
 Gazint
Gazint
Figure 11 Least-squares interpolation with Gazdag operator:
(a) The original wavefield generated by Gazdag modeling
for the synthetic model shown in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (a),
(b) The subsampled wavefield obtained by
zapping every other trace in
Figure
(a),
(b) The subsampled wavefield obtained by
zapping every other trace in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (a),
(c) The interpolated subsurface image obtained
by Gazdag migration,
(d) The interpolated subsurface image obtained
by least-squares Gazdag migration
(after 10 iterations).
(a),
(c) The interpolated subsurface image obtained
by Gazdag migration,
(d) The interpolated subsurface image obtained
by least-squares Gazdag migration
(after 10 iterations).






Next: CONCLUSION
Up: Ji: LS imaging, datuming
Previous: LEAST-SQUARES DATUMING
Stanford Exploration Project
11/17/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (a),
a synthetic model was generated using the Kirchhoff modeling operator
and the subsampled by zapping every other trace.
The result of modeling is shown in Figure
(a),
a synthetic model was generated using the Kirchhoff modeling operator
and the subsampled by zapping every other trace.
The result of modeling is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (b).
By applying the conjugate operator,
(b).
By applying the conjugate operator, ![]() , to the subsampled
data, we get an interpolated image, as shown in Figure
, to the subsampled
data, we get an interpolated image, as shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (c).
It is very difficult to distinguish the effect of
the subsampling operator from the artifacts of the Kirchhoff
operator, but we can see that this image is very similar to the image
obtained without the subsampling operator shown in Figure
(c).
It is very difficult to distinguish the effect of
the subsampling operator from the artifacts of the Kirchhoff
operator, but we can see that this image is very similar to the image
obtained without the subsampling operator shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (c).
The image obtained by the least-squares interpolation is shown
in Figure
(c).
The image obtained by the least-squares interpolation is shown
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (d); it closely resembles the image
obtained from the data without subsampling.
(d); it closely resembles the image
obtained from the data without subsampling.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
This result also closely resembles that for the images
without subsampling.
The reason may be that the wavefront healing effect during
the extrapolation.
.
This result also closely resembles that for the images
without subsampling.
The reason may be that the wavefront healing effect during
the extrapolation.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (b),
(b) The subsampled wavefield.
(c) The interpolated subsurface image obtained
by Kirchhoff migration with a subsampling operator,
(d) The interpolated subsurface image obtained
by least-squares Kirchhoff interpolation
(after 10 iterations).
(b),
(b) The subsampled wavefield.
(c) The interpolated subsurface image obtained
by Kirchhoff migration with a subsampling operator,
(d) The interpolated subsurface image obtained
by least-squares Kirchhoff interpolation
(after 10 iterations).
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (a),
(b) The subsampled wavefield obtained by
zapping every other trace in
Figure
(a),
(b) The subsampled wavefield obtained by
zapping every other trace in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (a),
(c) The interpolated subsurface image obtained
by Gazdag migration,
(d) The interpolated subsurface image obtained
by least-squares Gazdag migration
(after 10 iterations).
(a),
(c) The interpolated subsurface image obtained
by Gazdag migration,
(d) The interpolated subsurface image obtained
by least-squares Gazdag migration
(after 10 iterations).