




Next: LEAST-SQUARES INTERPOLATION
Up: Ji: LS imaging, datuming
Previous: Finite-difference migration in v(x,z)
Datuming is a method of processing to extrapolate a known
wavefield at a specified datum of arbitrary shape
to another specified datum, also of arbitrary shape.
Ji and Claerbout (1992) presented a datuming algorithm
based on the phase-shift depth extrapolation elsewhere in this report.
In the datuming problem, we use upward and downward extrapolation operators
instead of the modeling and migration operators.
For a given wavefield on the irregular surface, we can estimate
new wavefield on a datum by minimizing the errors between the
given input and the data modeled by the extrapolation, as follows:
| 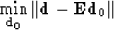 |
(7) |
where 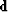 is a given wavefield on an irregular topography,
is a given wavefield on an irregular topography,
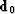 is a wavefield on a new datum,
and
is a wavefield on a new datum,
and 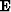 represents an extrapolation operator either upward or downward.
For example, if a new datum is located above the given datum,
the extrapolation operator
represents an extrapolation operator either upward or downward.
For example, if a new datum is located above the given datum,
the extrapolation operator 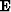 will be
the downward extrapolation operator.
will be
the downward extrapolation operator.
For demonstration, the phase shift datuming operator,
explained by Ji and Claerbout (1992), was used.
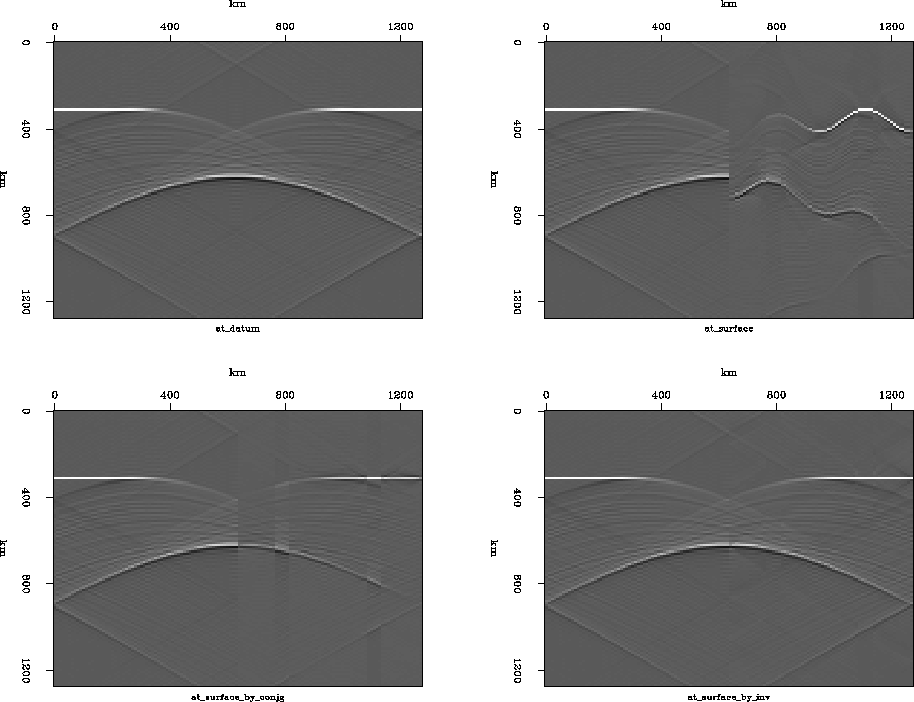
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (a) is the wavefield on a datum.
This wavefield was extrapolated to the nonflat surface shown
in Figure
(a) is the wavefield on a datum.
This wavefield was extrapolated to the nonflat surface shown
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (a), and the wavefield on the nonflat
surface is shown in Figure
(a), and the wavefield on the nonflat
surface is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (b).
The purpose is to datum the wavefield to the original surface.
By using the downward extrapolation operator,
I obtained datumed wavefield;
the result is shown in Figure
(b).
The purpose is to datum the wavefield to the original surface.
By using the downward extrapolation operator,
I obtained datumed wavefield;
the result is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (c).
Compared to the original wavefield, the datumed wavefield
is correctly positioned,
but you can see that the amplitude of the datumed
wavefield is different from that of the original wavefield.
Figure
(c).
Compared to the original wavefield, the datumed wavefield
is correctly positioned,
but you can see that the amplitude of the datumed
wavefield is different from that of the original wavefield.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (d) shows the datumed wavefield obtained by using
the least-squares datuming method.
It has a very nice amplitude recovery.
(d) shows the datumed wavefield obtained by using
the least-squares datuming method.
It has a very nice amplitude recovery.
Dtminv
Figure 9 Least-squares inverse datuming:
(a) Wave field on the datum surface.
(b) Wave field on the undulating surface shown in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (a),
(c) Datumed wavefield from the undulating surface
shown in (b),
(d) wavefield obtained by the least-squares inverse
datuming from the undulating surface shown in
(b) (after 10 iterations).
(a),
(c) Datumed wavefield from the undulating surface
shown in (b),
(d) wavefield obtained by the least-squares inverse
datuming from the undulating surface shown in
(b) (after 10 iterations).






Next: LEAST-SQUARES INTERPOLATION
Up: Ji: LS imaging, datuming
Previous: Finite-difference migration in v(x,z)
Stanford Exploration Project
11/17/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (a) is the wavefield on a datum.
This wavefield was extrapolated to the nonflat surface shown
in Figure
(a) is the wavefield on a datum.
This wavefield was extrapolated to the nonflat surface shown
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (a), and the wavefield on the nonflat
surface is shown in Figure
(a), and the wavefield on the nonflat
surface is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (b).
The purpose is to datum the wavefield to the original surface.
By using the downward extrapolation operator,
I obtained datumed wavefield;
the result is shown in Figure
(b).
The purpose is to datum the wavefield to the original surface.
By using the downward extrapolation operator,
I obtained datumed wavefield;
the result is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (c).
Compared to the original wavefield, the datumed wavefield
is correctly positioned,
but you can see that the amplitude of the datumed
wavefield is different from that of the original wavefield.
Figure
(c).
Compared to the original wavefield, the datumed wavefield
is correctly positioned,
but you can see that the amplitude of the datumed
wavefield is different from that of the original wavefield.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (d) shows the datumed wavefield obtained by using
the least-squares datuming method.
It has a very nice amplitude recovery.
(d) shows the datumed wavefield obtained by using
the least-squares datuming method.
It has a very nice amplitude recovery.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (a),
(c) Datumed wavefield from the undulating surface
shown in (b),
(d) wavefield obtained by the least-squares inverse
datuming from the undulating surface shown in
(b) (after 10 iterations).
(a),
(c) Datumed wavefield from the undulating surface
shown in (b),
(d) wavefield obtained by the least-squares inverse
datuming from the undulating surface shown in
(b) (after 10 iterations).