




Next: The vectorizer operator
Up: THEORETICAL BACKGROUND
Previous: Uncoupling the downgoing and
It is easy to obtain the horizontal component of the gradient in the
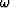 -
-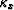 domain
domain
| 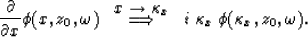 |
(13) |
To obtain the vertical component however, it is necessary to uncouple the
downgoing and upcoming components. Taking the vertical derivative of
equation (5), moving to the 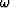 -
-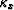 domain, and
using the relations in (7), we get
domain, and
using the relations in (7), we get
| 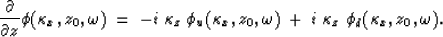 |
(14) |
Finally, equations (11) and (12) can be
substituted into equation (14) to give
| 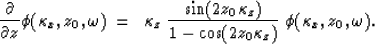 |
(15) |
A first glance at equation (15) shows that it has a set
of singular strings in the 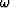 -
-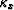 plane, which are defined
by
plane, which are defined
by
| ![\begin{displaymath}
\omega_n(\kappa_x) = \pm \sqrt{\left({K \over \rho}\right) \left[
\left({n \pi \over z_0}\right)^2 + \kappa_x^2 \right]},\end{displaymath}](img28.gif) |
(16) |
and which correspond to vertical wavelengths of 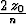 .For waves with these wavelengths, the downgoing and upcoming fields
cancel each other at the cable depth (assuming perfect reflection
at the water's surface), and the result is a zero in the recorded wavefield.
Nevertheless, this cancellation does not restrict the complete recovery of
the displacement field because, fortunately, the associated singularities
are removable.
.For waves with these wavelengths, the downgoing and upcoming fields
cancel each other at the cable depth (assuming perfect reflection
at the water's surface), and the result is a zero in the recorded wavefield.
Nevertheless, this cancellation does not restrict the complete recovery of
the displacement field because, fortunately, the associated singularities
are removable.
In the neighborhood of these strings, the vertical component of the
pressure gradient is given by
| 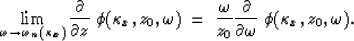 |
(17) |





Next: The vectorizer operator
Up: THEORETICAL BACKGROUND
Previous: Uncoupling the downgoing and
Stanford Exploration Project
11/18/1997
![]() -
-![]() plane, which are defined
by
plane, which are defined
by
![\begin{displaymath}
\omega_n(\kappa_x) = \pm \sqrt{\left({K \over \rho}\right) \left[
\left({n \pi \over z_0}\right)^2 + \kappa_x^2 \right]},\end{displaymath}](img28.gif)