




Next: Calculating the pressure gradient
Up: THEORETICAL BACKGROUND
Previous: Relating the pressure and
Most of the treatment that follows is carried out
either in the  -p or in the
-p or in the 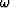 -
-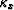 domain. To simplify
the analysis, avoiding the unnecessary intrusion of convolutions along
the
domain. To simplify
the analysis, avoiding the unnecessary intrusion of convolutions along
the 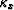 axis, the discussion focuses on the points in space
where the wavefield is measured, that is, at the points (x,z = z0) where
z0 is the cable depth. At these points the bulk moduli and density
are constant and known: K(x,z0)=K, and
axis, the discussion focuses on the points in space
where the wavefield is measured, that is, at the points (x,z = z0) where
z0 is the cable depth. At these points the bulk moduli and density
are constant and known: K(x,z0)=K, and 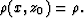
The pressure field 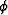 at any position of the space can be represented
as the superposition of an upward propagating wavefield
at any position of the space can be represented
as the superposition of an upward propagating wavefield 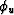 with a
downward propagating wavefield
with a
downward propagating wavefield 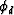 :
:
| 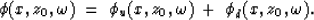 |
(5) |
Continuation of these wavefields in the frequency-horizontal wavenumber
domain (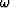 -
-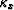 ) is controlled by the following equations:
) is controlled by the following equations:
| 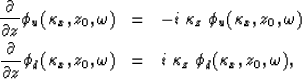 |
(6) |
| (7) |
where 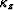 is the vertical wavenumber, which relates to the
horizontal slowness p through the dispersion relation
is the vertical wavenumber, which relates to the
horizontal slowness p through the dispersion relation
| 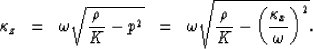 |
(8) |
To separate these two wavefields, we must make the following assumptions:
- The water-air reflection coefficient
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) is
is 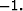
- The water surface is nearly horizontal.
- The cable depth is a smooth function of the receiver position.
Under these assumptions, the upcoming and downgoing fields can be related by
a simple time shift equation in the  -p domain:
-p domain:
| 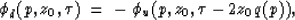 |
(9) |
where q is the vertical slowness. When the source is located
below the cable equation (9) can be applied without
restrictions, and the only event for which it doesn't hold perfectly true,
for cases in which the source is above the cable, is the direct wave.
Substituting equation (9) into equation (5),
both in the 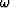 -p domain, we obtain
-p domain, we obtain
| ![\begin{displaymath}
\phi(p,z_0,\omega) \; = \; \phi_u(p,z_0,\omega) \; [ 1 - \exp{(i 2 z_0 \omega
\sqrt{\rho/K - p^2})} ];\end{displaymath}](img22.gif) |
(10) |
which results in the following equations for separation of the
two wavefields:
| 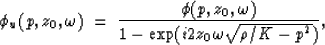 |
(11) |
| 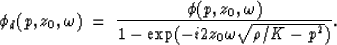 |
(12) |





Next: Calculating the pressure gradient
Up: THEORETICAL BACKGROUND
Previous: Relating the pressure and
Stanford Exploration Project
11/18/1997
![]() at any position of the space can be represented
as the superposition of an upward propagating wavefield
at any position of the space can be represented
as the superposition of an upward propagating wavefield ![]() with a
downward propagating wavefield
with a
downward propagating wavefield ![]() :
:
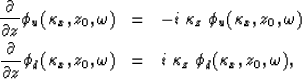
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) is
is ![]() -p domain, we obtain
-p domain, we obtain