




Next: Calculating the phase spectrum
Up: THEORY
Previous: THEORY
We choose the convention that the picking position of a wavelet is
the first break of the minimum phase part and the ending point of
the maximum phase part. The minimum phase
part is causal and the maximum phase part is anti-causal:
| 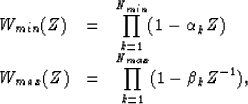 |
(4) |
where 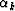 and
and 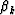 are generally complex with their norm
less than one, and Nmin+Nmax=N. Clearly, this choice ensures that
for a minimum phase wavelet, the first break of the wavelet is picked, and that
for a zero phase wavelet, the center point of the wavelet is picked.
are generally complex with their norm
less than one, and Nmin+Nmax=N. Clearly, this choice ensures that
for a minimum phase wavelet, the first break of the wavelet is picked, and that
for a zero phase wavelet, the center point of the wavelet is picked.
To estimate n0, we need to examine the phase response of S(Z).
Let 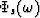 be the phase spectrum of
be the phase spectrum of 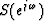 ,and
,and 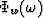 the phase spectrum of
the phase spectrum of 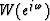 .
Equating the the phase spectra of the two sides of equation (3)
yields
.
Equating the the phase spectra of the two sides of equation (3)
yields
| 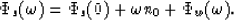 |
(5) |
Because w(n) is a real sequence and has causal minimum phase and
anti-causal maximum phase parts, its phase spectrum is anti-symmetric
with respect to 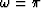 :
:
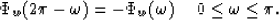
Using this condition, we can solve equation (5) for n0
as follows:
| ![\begin{displaymath}
n_0 = {1 \over 2\pi}[\Phi_s(2\pi-\omega)+\Phi_s(\omega)-2\Phi_s(0)].\end{displaymath}](img13.gif) |
(6) |
By setting 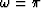 , we see that n0 is the phase delay of the
received signal at the Nyquist frequency:
, we see that n0 is the phase delay of the
received signal at the Nyquist frequency:
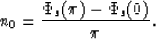





Next: Calculating the phase spectrum
Up: THEORY
Previous: THEORY
Stanford Exploration Project
12/18/1997
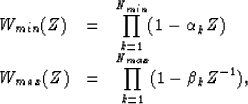
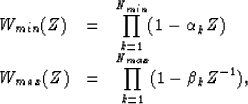
![]() be the phase spectrum of
be the phase spectrum of ![]() ,and
,and ![]() the phase spectrum of
the phase spectrum of ![]() .
Equating the the phase spectra of the two sides of equation (3)
yields
.
Equating the the phase spectra of the two sides of equation (3)
yields
![]()
![]()