THEORY

Let w(n) be a source wavelet of length N. Its Z-transform can be factorized into a minimum phase part and a maximum phase part as follows:

W(Z) = W_min(Z)W_max(Z),

if none of its zeros are exactly on the unit circle. The received signal can be modeled as a delayed source wavelet as follows:

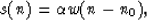$$s(n) = \alpha w(n-n_0),$$ (2)

or in the frequency domain,

 

S(Z)=C W(Z)Z^n₀, (3)

where C is a constant. The amount of delay n₀ is equal to the traveltime it takes for the wavelet to propagate from the source location to the receiver location. This equation shows that traveltime picking can be equivalently accomplished by estimating n₀.