EIGENVECTOR FORMULATION OF MISSING DATA PROBLEM

There are unknowns in a vector $\bold m$and knowns in a vector $\bold k$.Pack $\bold m$ and $\bold k$into a column vector $\bold d$ which will be known as ``data space''. There is also a known linear operator $\bold A$,and I have programs that will rapidly evaluate $\bold A \bold d$ and $\bold A' \bold r$ for any vectors $\bold d$ and $\bold r$.Here $\bold A'$ denotes the conjugate of $\bold A$.

 

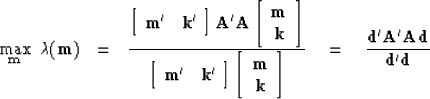
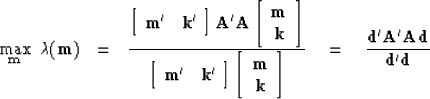$$\max_{\bold m} \ \lambda({\bold m}) \ \ =\ \ { \left[ \begi... ...\ \ \ {\bold d' \bold A'\bold A \bold d \over \bold d' \bold d}$$ (1)

In the physical problem, the components of $\bold m$ and $\bold k$ randomly interleave one another and there are huge numbers of components of each. To gain some insight and see how classical mathematics is relevant, forget for a moment the distinction between known and missing data and imagine that all the components of the data field $\bold d$are independent variables. Then, it is well known (and I will repeat the proof below) that the stationary values of $\lambda$ in (1) are the family of eigenvalues. So if components of $\bold k$ happen to be components of the eigenvector of maximum eigenvalue, then maximization of $\bold \lambda$ will bring $\bold m$to the remaining components of that eigenvector of maximum eigenvalue. My conjecture is that in practice we would find that maximization of $\bold \lambda$would lead to estimated missing data $\bold m$that best fits the various components in the known data $\bold k$.

In many of our applications, $\bold A$ is roughly a unitary matrix because it arises from wave propagation problems. Think of $\lambda$ this way: The denominator limits the total energy; In such cases, maximization should quickly exclude evanescent energy, but a huge number of eigenvalues are all the same, so the maximization is extremely nonunique. To obtain uniqueness with unitary operators we need to introduce a weighting function such as $\lambda(\bold m )=(\bold d' \bold A'\bold W\bold A \bold d)/(\bold d'\bold d)$.

The mathematical problem with the $\bold k$ constraints however, was unknown to Michael Saunders. Since it is a nonlinear problem we should be wary of multiple unwanted solutions, but that need not stop us from trying. My proposed method for the optimization (1) follows from what I know about conjugate gradients: First we easily find a gradient and keep a vector representing the previous step. Second, scaling these by $\alpha$ and $\beta$ respectively, $\lambda(\alpha,\beta )$ is a simple ratio of quadratic forms in two variables. After getting the coefficients of these quadratic forms the problem is of such low dimensionality (two) that almost any method should suffice.