




Next: CODING
Up: Claerbout: Eigenvectors for missing
Previous: EIGENVECTOR FORMULATION OF MISSING
The gradient of 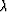 will assist us in finding the maximum.
First recall the derivative of a quotient:
will assist us in finding the maximum.
First recall the derivative of a quotient:
| 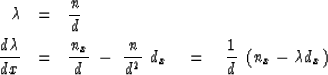 |
(2) |
| (3) |
Using (3)
we set to zero the gradient of the quadratic form
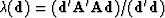 getting
getting
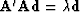 which proves the eigenvector assertion I made above.
which proves the eigenvector assertion I made above.
Now restate the gradient
while distinguishing missing data from known data
and taking the gradient only with respect to the missing.
To exhibit this most clearly,
we write the 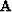 operator with
its columns separated into two parts,
one for missing data and one for known,
operator with
its columns separated into two parts,
one for missing data and one for known,
![$ \bold A = [ \bold B \bold C ]$](img19.gif)
| ![\begin{displaymath}
{ \partial \lambda \over \partial \bold m'}
\ \ \ =\ \ \
\bo...
...
\bold m \\ \bold k\end{array}\right]
\ \ - \ \ \lambda \bold m\end{displaymath}](img20.gif) |
(4) |
Another expression for the gradient offers more insight
and is often more practical during coding:
Let 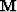 be a square matrix with ones and zeros on
the main diagonal where ones are found at locations of missing
data and zeros otherwise.
Using
be a square matrix with ones and zeros on
the main diagonal where ones are found at locations of missing
data and zeros otherwise.
Using 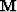 ,the gradient is
,the gradient is
| ![\begin{displaymath}
\bold g \ \ \ =\ \ \\ bold M
\left[ \bold A'\bold A \bold d ...
...arallel \over
\parallel \bold d \parallel
} \ \bold d
\right]\end{displaymath}](img22.gif) |
(5) |





Next: CODING
Up: Claerbout: Eigenvectors for missing
Previous: EIGENVECTOR FORMULATION OF MISSING
Stanford Exploration Project
12/18/1997
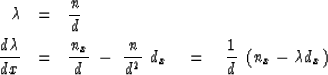
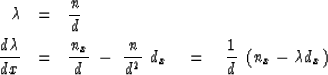
![]() operator with
its columns separated into two parts,
one for missing data and one for known,
operator with
its columns separated into two parts,
one for missing data and one for known,
![]()