Next: Accuracy
Up: Ji and Biondi: Explicit
Previous: ONE-WAY WAVE EQUATION AND
The first-order approximations of the one-way wave equation by both
continued-fraction expansion and Taylor-series expansion result
in the same equation: the conventional 15-degree equation.
The 15-degree migration equation in the 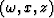 domain (Claerbout, 1985) is given by
domain (Claerbout, 1985) is given by
| 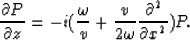 |
(6) |
After a second difference approximation to the second partial derivative
and subsequent simplification, the equation (6) becomes
| 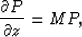 |
(7) |
where the matrix M takes the form
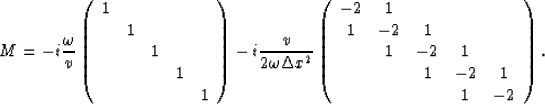
Rearranging,
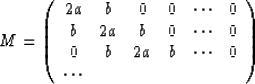
with
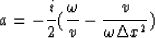
and
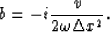
The solution to equation (7) is
| 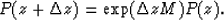 |
(8) |
The calculation of the exponentiated matrix 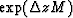 requires matrix
diagonalization, which is numerically expensive.
However, we can approximate the exponential of the matrix by
writing (Richardson, et al., 1991)
requires matrix
diagonalization, which is numerically expensive.
However, we can approximate the exponential of the matrix by
writing (Richardson, et al., 1991)
|  |
(9) |
where the matrix M is split into two matrices M=Me+Mo, with

and

The approximate depth-stepping operator,
| 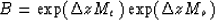 |
(10) |
forms the basis for our unconditionally stable, explicit algorithm for
migration. To compute the matrix exponentials, notice that both Me
and Mo are block diagonal and we need only consider the exponential
of the 2 by 2 matrix
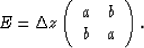
By using the eigenvalue decomposition of the matrix, we see that
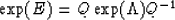
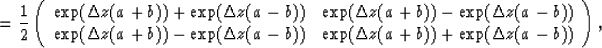
where Q represents the matrix whose columns are eigenvectors of the
matrix E, and 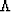 is the diagonal eigenvalue matrix.
is the diagonal eigenvalue matrix.
Since both Me and Mo are block diagonal, exponentiating them amounts to
exponentiating E. Both 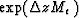 and
and 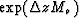 are also block diagonal. Since the eigenvalues of
are also block diagonal. Since the eigenvalues of 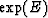 are
are 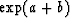 and
and 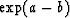 with a and b imaginary, it follows that
with a and b imaginary, it follows that
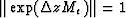 and
and 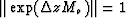 .To prove the unconditional stability of the algorithm we need only show that
.To prove the unconditional stability of the algorithm we need only show that
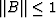 . This follows immediately since
. This follows immediately since 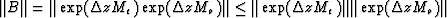 , each of
which 1 according to the preceding discussion.
, each of
which 1 according to the preceding discussion.
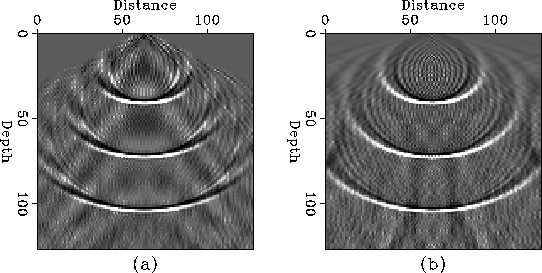
In Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , the impulse responses of both implicit and
explicit operators of 15-degree migration are compared for the same
extrapolation step
, the impulse responses of both implicit and
explicit operators of 15-degree migration are compared for the same
extrapolation step 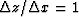 .
In the case of the implicit scheme, we used a Crank-Nicholson
implementation which has an accuracy on the order of
.
In the case of the implicit scheme, we used a Crank-Nicholson
implementation which has an accuracy on the order of 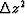 .For the explicit scheme, we performed a second-order approximation
using a split M = Me + Mo whose accuracy is on the order of
.For the explicit scheme, we performed a second-order approximation
using a split M = Me + Mo whose accuracy is on the order of 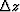 .We see that the impulse response
of the explicit method has the shape of an ellipse, which is
characteristic of the 15-degree extrapolation operator.
The impulse response of the explicit method shows some dispersion
than that of the implicit scheme due to a poor approximation of
the matrix exponent.
The way to get a more accurate approximation is discussed
in the following section.
.We see that the impulse response
of the explicit method has the shape of an ellipse, which is
characteristic of the 15-degree extrapolation operator.
The impulse response of the explicit method shows some dispersion
than that of the implicit scheme due to a poor approximation of
the matrix exponent.
The way to get a more accurate approximation is discussed
in the following section.
fig1
Figure 1 The impulse responses (a) of explicit 15-degree migration
with split M = Me + Mo and (b) of implicit 15-degree migration with
Crank-Nicholson approximation. Both extrapolations are performed with the
same extrapolation step 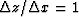 .
.










Next: Accuracy
Up: Ji and Biondi: Explicit
Previous: ONE-WAY WAVE EQUATION AND
Stanford Exploration Project
12/18/1997
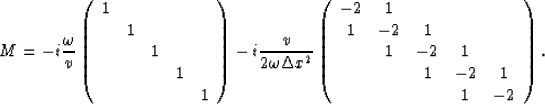
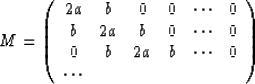
![]()
![]()


![]()
![]()
![]()
![]() and
and ![]() are also block diagonal. Since the eigenvalues of
are also block diagonal. Since the eigenvalues of ![]() are
are ![]() and
and ![]() with a and b imaginary, it follows that
with a and b imaginary, it follows that
![]() and
and ![]() .To prove the unconditional stability of the algorithm we need only show that
.To prove the unconditional stability of the algorithm we need only show that
![]() . This follows immediately since
. This follows immediately since ![]() , each of
which 1 according to the preceding discussion.
, each of
which 1 according to the preceding discussion.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , the impulse responses of both implicit and
explicit operators of 15-degree migration are compared for the same
extrapolation step
, the impulse responses of both implicit and
explicit operators of 15-degree migration are compared for the same
extrapolation step ![]() .
In the case of the implicit scheme, we used a Crank-Nicholson
implementation which has an accuracy on the order of
.
In the case of the implicit scheme, we used a Crank-Nicholson
implementation which has an accuracy on the order of ![]() .For the explicit scheme, we performed a second-order approximation
using a split M = Me + Mo whose accuracy is on the order of
.For the explicit scheme, we performed a second-order approximation
using a split M = Me + Mo whose accuracy is on the order of ![]() .We see that the impulse response
of the explicit method has the shape of an ellipse, which is
characteristic of the 15-degree extrapolation operator.
The impulse response of the explicit method shows some dispersion
than that of the implicit scheme due to a poor approximation of
the matrix exponent.
The way to get a more accurate approximation is discussed
in the following section.
.We see that the impulse response
of the explicit method has the shape of an ellipse, which is
characteristic of the 15-degree extrapolation operator.
The impulse response of the explicit method shows some dispersion
than that of the implicit scheme due to a poor approximation of
the matrix exponent.
The way to get a more accurate approximation is discussed
in the following section.