




Next: 15-DEGREE DEPTH MIGRATION
Up: Ji and Biondi: Explicit
Previous: Introduction
Most extrapolation methods used in migration and modeling
are based on the scalar wave equation. For a 2-D acoustic earth model, the
two-way scalar wave equation in the 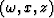 domain is of the following
form:
domain is of the following
form:
| 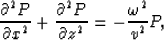 |
(1) |
where P is the pressure field, 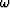 is the frequency, z is depth,
and v is velocity.
Solving the scalar wave equation requires the first depth derivative of the
wavefield. To obtain a one-way solution to the two-way equation,
without having to know the vertical derivatives,
we can use the one-way scalar wave equation
is the frequency, z is depth,
and v is velocity.
Solving the scalar wave equation requires the first depth derivative of the
wavefield. To obtain a one-way solution to the two-way equation,
without having to know the vertical derivatives,
we can use the one-way scalar wave equation
| 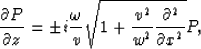 |
(2) |
where the positive sign is used in modeling, the negative sign in migration,
and the velocity is half of the true velocity.
While the one-way equation eliminates the need to know
the vertical derivatives of the wavefields, it contains a square-root
of a differential operator that cannot easily be implemented numerically.
There are two methods of rationalizing the square-root equation: by
Taylor series and by continued-fraction (Claerbout, 1985).
The Taylor-series method leads to an explicit scheme
whereas the continued-fraction method leads an implicit scheme.
The continued-fraction expansion was first used by Muir (Claerbout, 1985)
to approximate the square-root operator,
| 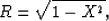 |
(3) |
where
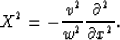
The expansion is
| 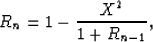 |
(4) |
where n is the order of approximation, and usually R0=1 (Claerbout, 1985).
In implicit algorithms, the fraction expansion method for approximation is
implemented recursively.
In the explicit scheme this method makes implementation difficult
because it produces another function of a matrix and as a result,
a Taylor-series expansion is generally used. By Taylor-series expansion,
the square root operator given in equation (3)
can be written as
| 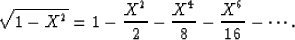 |
(5) |





Next: 15-DEGREE DEPTH MIGRATION
Up: Ji and Biondi: Explicit
Previous: Introduction
Stanford Exploration Project
12/18/1997
![]()