Next: Lateral velocity variation
Up: 15-DEGREE DEPTH MIGRATION
Previous: 15-DEGREE DEPTH MIGRATION
From the series definition of a matrix function, we see that the matrix
exponential can be represented as follows:
|  |
(11) |
Richardson, et al. approximate this matrix exponential
by splitting the given matrix into pieces:
|  |
(12) |
Equation (12) can be represented with the series
|  |
(13) |
|  |
(14) |
An approximate calculation of equation (13) is
|  |
(15) |
|  |
(16) |
|  |
(17) |
Equation (14) and (15) are identical if Me and Mo are commutative,
i.e., 2MeMo = MeMo + MoMe.
However, in our case, Me and Mo are not commutative,
thus approximation (15) will have errors
on the order of  .By careful arrangement of two different split matrices,
we can improve the accuracy as follows.
We define
.By careful arrangement of two different split matrices,
we can improve the accuracy as follows.
We define
|  |
(18) |
which has an error on the order of  , and
, and
|  |
(19) |
with an error on the order of  .
.
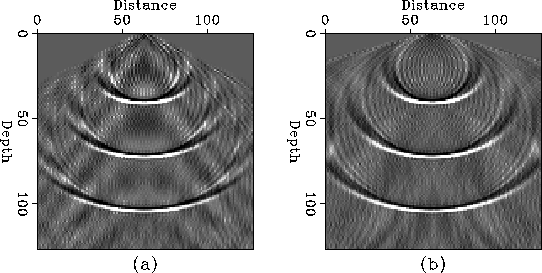
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the improvement in accuracy when we use
a higher order approximation.
On the left impulse response, we used the first order approximation with
split as equation (18) and on the right impulse response, we used
the third order approximation as equation (19). We can see a decrease
in the dispersion at higher order approximation.
Comparing with the impulse response of implicit scheme in Fig
shows the improvement in accuracy when we use
a higher order approximation.
On the left impulse response, we used the first order approximation with
split as equation (18) and on the right impulse response, we used
the third order approximation as equation (19). We can see a decrease
in the dispersion at higher order approximation.
Comparing with the impulse response of implicit scheme in Fig ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
the higher order explicit scheme shows the comparable accuracy as we can see
in Fig
,
the higher order explicit scheme shows the comparable accuracy as we can see
in Fig ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
fig2
Figure 2 Impulse responses of explicit 15-degree migration with the split matrices (a) M = Me+Mo, (b) M = Me/4+Mo/2+Me/2+Mo/2+Me/4.










Next: Lateral velocity variation
Up: 15-DEGREE DEPTH MIGRATION
Previous: 15-DEGREE DEPTH MIGRATION
Stanford Exploration Project
12/18/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the improvement in accuracy when we use
a higher order approximation.
On the left impulse response, we used the first order approximation with
split as equation (18) and on the right impulse response, we used
the third order approximation as equation (19). We can see a decrease
in the dispersion at higher order approximation.
Comparing with the impulse response of implicit scheme in Fig
shows the improvement in accuracy when we use
a higher order approximation.
On the left impulse response, we used the first order approximation with
split as equation (18) and on the right impulse response, we used
the third order approximation as equation (19). We can see a decrease
in the dispersion at higher order approximation.
Comparing with the impulse response of implicit scheme in Fig ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
the higher order explicit scheme shows the comparable accuracy as we can see
in Fig
,
the higher order explicit scheme shows the comparable accuracy as we can see
in Fig ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.