Next: Use of the conjugate
Up: THE FINITE ELEMENT METHOD
Previous: A model problem
The basis functions I use are bilinear functions. The nodal basis
function for the ith node Ni has the value 1 at
node i, zero at all other nodes, and is a bilinear function in between.
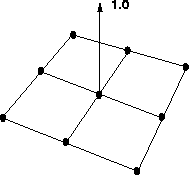
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the basis function for one node. The
element Ai,j of the Galerkin operator is the integral of the dot product
of the gradient of the basis functions for the ith and jth
nodes. The basis function for the ith node is only non-zero in the
four elements that have node i as a vertex. Thus, the only non-zero
elements of the operator are Ai,j where nodes i and j
are vertices of a common element.
shows the basis function for one node. The
element Ai,j of the Galerkin operator is the integral of the dot product
of the gradient of the basis functions for the ith and jth
nodes. The basis function for the ith node is only non-zero in the
four elements that have node i as a vertex. Thus, the only non-zero
elements of the operator are Ai,j where nodes i and j
are vertices of a common element.
nodaldiag
Figure 2 The basis function for a node is one at the node and only non-zero in the four elements connected to the node.

Almost all FE codes try to avoid constructing the full Galerkin operator
because it is a very sparse matrix. Instead they construct local operators for
each element. In the model problem the element operator is a 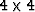 matrix, where the elements are the evaluation of the integral a(Ni,Nj)
over the element. Here, i and j run from 1 to 4, the local node numbering
for the element. The global operator is formed as a sum of the element
matrices. The application of the operator can be performed as a three stage
operation,
matrix, where the elements are the evaluation of the integral a(Ni,Nj)
over the element. Here, i and j run from 1 to 4, the local node numbering
for the element. The global operator is formed as a sum of the element
matrices. The application of the operator can be performed as a three stage
operation,
- 1.
- spread the nodal values to form a 4-vector for each element,
- 2.
- parallel application of the element matrices,
- 3.
- gather the RHS 4-vector values and sum into the output vector.
This is the standard way that unassembled Galerkin operators are
applied on vector computers (Ferencz, 1989). These calculations are
performed for each element so the vector length is the total
number of elements.





Next: Use of the conjugate
Up: THE FINITE ELEMENT METHOD
Previous: A model problem
Stanford Exploration Project
12/18/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the basis function for one node. The
element Ai,j of the Galerkin operator is the integral of the dot product
of the gradient of the basis functions for the ith and jth
nodes. The basis function for the ith node is only non-zero in the
four elements that have node i as a vertex. Thus, the only non-zero
elements of the operator are Ai,j where nodes i and j
are vertices of a common element.
shows the basis function for one node. The
element Ai,j of the Galerkin operator is the integral of the dot product
of the gradient of the basis functions for the ith and jth
nodes. The basis function for the ith node is only non-zero in the
four elements that have node i as a vertex. Thus, the only non-zero
elements of the operator are Ai,j where nodes i and j
are vertices of a common element.