Next: A model problem Up: Nichols: Finite elements on Previous: Introduction

THE FINITE ELEMENT METHOD

Since the FE method has not been discussed much in SEP reports, I will now attempt to give a general introduction to the method. If you are a FE expert the generalizations and omissions in this description may offend you so you should skip to the next section.

The FE method for solving a partial differential equation starts by casting the P.D.E. as a variational problem. The differential problem

$\begin{eqnarraystar} F(u) = f & {\rm on} & \Omega \cr u = g & {\rm on} & \parti... ...rtial u \over \partial n} = h &{\rm on} & \partial\Omega_2 \cr\end{eqnarraystar}$

may be expressed as the variational problem, find $u\in V$ such that,

$\begin{eqnarraystar} a(u,v) = (f,v) + <h,v\gt && \forall v\in V \cr (f,v)=\int_\... ... f\,v\, dV, && <h,v\gt = \int_{\partial\Omega_2} h\,v\, dS \cr\end{eqnarraystar}$

where the space V and the form of the function a(u,v) depend on the differential operator F and the boundary conditions.

This is a variational problem in an infinite space, V. The approximate solution is obtained by restricting the search to a finite space of dimension k,V_k. The problem then becomes. Find u_k in V_k such that

$\begin{eqnarraystar} a(u_k,v_k) = (f,v_k) + <h,v_k\gt && \forall v_k\in V_k \cr ... ...k\, dV, && <h,v_k\gt = \int_{\partial\Omega_2} g\,v_k\, dS \cr\end{eqnarraystar}$

The accuracy of the solutions depends on the distance of the true solution u from the solution in the finite space u_k.

If we construct a set of basis functions, $\phi_i,i=1,k$ that spans the space V_k, the problem can be rewritten as find $u_k \in V_k$ such that,

$\begin{eqnarraystar} a(u_k,\phi_i) = (f,\phi_i) + <h,\phi_i\gt && i=1,\cdots,k\end{eqnarraystar}$

If the function u_k is written as a linear combination of the basis functions 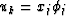$u_k = x_j\phi_j$ , we have,

$\begin{eqnarraystar} a(\phi_j,\phi_i) x_j = (f,\phi_i) + <h,\phi_i\gt && i=1,\cdots,k\end{eqnarraystar}$

This is a linear problem for the scalars x_j of the form Ax=b with,

$\begin{displaymath} A_{ij} = a(\phi_j,\phi_i),\ \ b_i = (f,\phi_i) + <h,\phi_i\gt\end{displaymath}$

This system of equations is know as the Galerkin system. If the basis functions are chosen to be orthogonal in the metric defined by the function $a(\phi_j,\phi_i)$ , then the matrix A is diagonal. Unfortunately, for irregular problems, such functions are difficult to construct. In the FE method the functions are chosen to be functions with local support so that most elements of the matrix A are zero. The non-zero elements of A correspond to basis functions whose regions of support overlap. The basis functions are defined in terms of nodes of the elements.

The FE method has six basic stages:

1.: Construct a decomposition of the domain $\Omega$ into elements.
2.: Choose suitable basis functions. The basis functions are parameterized in terms of values at nodes in the elements. The nodes may be internal, on the edges, or at the vertices of an element. When using linear basis functions, as I do, the nodes are usually at the vertices of the elements.
3.: Calculation of the Galerkin system.
4.: Imposition of boundary conditions.
5.: Solution of the Galerkin system.

Next: A model problem Up: Nichols: Finite elements on Previous: Introduction

Stanford Exploration Project
12/18/1997