Next: Zero-offset migration
Up: 11: TRUE AMPLITUDE MIGRATION
Previous: 11: TRUE AMPLITUDE MIGRATION
To develop true-amplitude formulas for the CSP case, we shall use the
simple fact that if 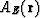 is the amplitude of the discontinuity
received as a result of wave-field continuation with the amplitude-equivalent
operator
is the amplitude of the discontinuity
received as a result of wave-field continuation with the amplitude-equivalent
operator 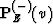 with the kernel
with the kernel
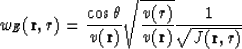
and if the kernel of the operator 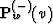 is
is
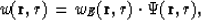
then as a result of applying the operator 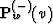 we receive the
amplitude
we receive the
amplitude
| 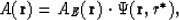 |
(117) |
(note that the star means that r* belongs to the same
ray
of eiconal  as r).
as r).
But the operator 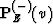 acts inversely (in the sense of
q-equivalence). This means that at the point
acts inversely (in the sense of
q-equivalence). This means that at the point  on the reflector,
on the reflector,
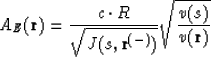
where 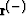 means the point
means the point  before the reflection.
before the reflection.
According to equation (117),
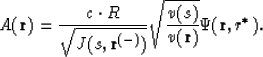
Now we apply the condition
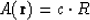
and receive
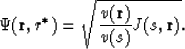
So the kernel we are looking for is
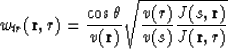
or in homogeneous media![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
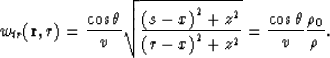
For land surveys, in the general case we have
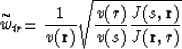
and in homogeneous media
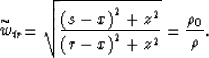





Next: Zero-offset migration
Up: 11: TRUE AMPLITUDE MIGRATION
Previous: 11: TRUE AMPLITUDE MIGRATION
Stanford Exploration Project
1/13/1998
![]()
![]()
![]() acts inversely (in the sense of
q-equivalence). This means that at the point
acts inversely (in the sense of
q-equivalence). This means that at the point ![]() on the reflector,
on the reflector,
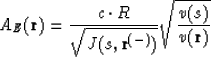
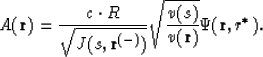
![]()
![]()
![]()
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
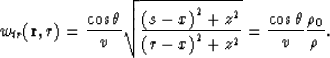
![]()