




Next: CSP migration, 3D case
Up: Goldin: Method of discontinuities
Previous: 10: EXTREMAL VELOCITIES
Our task will be to choose a kernel 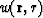 that supplies the
proportionality of image amplitude and reflection coefficient.
that supplies the
proportionality of image amplitude and reflection coefficient.
We shall neglect: 1) directional characteristics of the source,
2) refraction coefficients, 3) influence of the free boundary, and
4) variation of the density 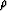 . With these restrictions the
amplitude of a wave on the surface
. With these restrictions the
amplitude of a wave on the surface 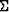 is:
is:
| 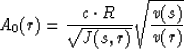 |
(116) |
where s and r are the source and receiver locations, 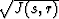 describes the geometrical spreading of a wave propagating along the
ray
describes the geometrical spreading of a wave propagating along the
ray 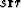 (see Figure 1), and R is the reflection coefficient at
the point
(see Figure 1), and R is the reflection coefficient at
the point  .
.
Equation (116) is good for marine surveys. For land surveys we usually measure
the vertical component
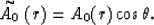





Next: CSP migration, 3D case
Up: Goldin: Method of discontinuities
Previous: 10: EXTREMAL VELOCITIES
Stanford Exploration Project
1/13/1998
![]() . With these restrictions the
amplitude of a wave on the surface
. With these restrictions the
amplitude of a wave on the surface ![]() is:
is:
![]()