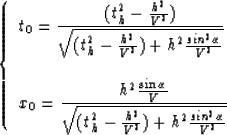
The PSPM operator defined in equations (1) can be written as function of the half-offset h, half-velocity V, and source-receiver travel time th:
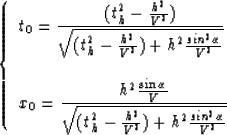 |
(2) |
Defining the variables
![]() ,we can rewrite equations
(2) as
,we can rewrite equations
(2) as
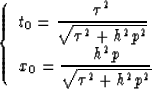 |
(3) |
Equations (3) are parametric
representations of the PSPM
operator, function of two new variables:
![]() and
and ![]() .The variable
.The variable ![]() is the
NMO corrected constant-offset travel
time, while the variable
is the
NMO corrected constant-offset travel
time, while the variable ![]() is the px=dt / dx parameter.
is the px=dt / dx parameter.
In Figure 1 the PSPM operator is mapped using
equations (3).
The elliptic curves
represent curves of constant ![]() parameter, while the
vertical curves are curves of constant
parameter, while the
vertical curves are curves of constant ![]() parameter.
The PSPM operator is represented by
parameter.
The PSPM operator is represented by ![]() and
and ![]() coordinates,
which is a velocity independent characterization. The velocity
cutoff is contained in the parameter
coordinates,
which is a velocity independent characterization. The velocity
cutoff is contained in the parameter ![]() , which is increasing toward
the edges of the plot.
, which is increasing toward
the edges of the plot.
The cutoff is determined by the parameter ![]() . Higher velocities
introduce the restriction in the parameter
. Higher velocities
introduce the restriction in the parameter ![]() which cannot be
higher than 1 / V, where V is half-velocity.
A medium with velocity V1 will have a
tighter cutoff than a medium with lower velocity V2, (V1 > V2).
In the first case the
which cannot be
higher than 1 / V, where V is half-velocity.
A medium with velocity V1 will have a
tighter cutoff than a medium with lower velocity V2, (V1 > V2).
In the first case the ![]() parameter takes values from to
1 / V1, (
parameter takes values from to
1 / V1, (![]() )
while in the second case the
)
while in the second case the
![]() parameter ranges from to 1 / V2
(
parameter ranges from to 1 / V2
(![]() ).
Two different media will share the same PSPM operator for the
same values of
).
Two different media will share the same PSPM operator for the
same values of ![]() . On the same DMO ellipse two media
with velocities V1,V2 migrate an impulse to the same place
if the equality
. On the same DMO ellipse two media
with velocities V1,V2 migrate an impulse to the same place
if the equality
![]() is satisfied. For a higher velocity medium, a high dip is migrated
in the same place as a lower dip in a lower velocity medium.
is satisfied. For a higher velocity medium, a high dip is migrated
in the same place as a lower dip in a lower velocity medium.
Equations (3) map the PSPM operator as a
function of the
variables ![]() and
and ![]() .
In a constant velocity medium, for each point in the
(
.
In a constant velocity medium, for each point in the
(![]() ,
, ![]() )space there corresponds a pair of values
(
)space there corresponds a pair of values
(![]() ,
, ![]() ) and vice-versa.
For a medium with variable velocity with depth V(z), it was
shown
that for certain velocity models the DMO impulse response
presents triplications
(Popovici and Biondi, 1989).
Supposing the PSPM operator is represented in a
system
of coordinates
(
) and vice-versa.
For a medium with variable velocity with depth V(z), it was
shown
that for certain velocity models the DMO impulse response
presents triplications
(Popovici and Biondi, 1989).
Supposing the PSPM operator is represented in a
system
of coordinates
(![]() ,
, ![]() ),
for certain velocity models
the transformation
),
for certain velocity models
the transformation
![]() is not unique, thus generating the triplications in the PSPM curve.
In a medium with variable velocity, this can be determined
by following the variation of the
is not unique, thus generating the triplications in the PSPM curve.
In a medium with variable velocity, this can be determined
by following the variation of the ![]() parameter along
the equal travel time reflector. When the value of
parameter along
the equal travel time reflector. When the value of ![]() is repeated along the same reflector with a given
is repeated along the same reflector with a given ![]() ,the PSPM operator will have multiple values of the
pair of parameters (x0,t0) for the same value of
,the PSPM operator will have multiple values of the
pair of parameters (x0,t0) for the same value of
![]() .According to this scheme it can be predicted for what
types of media the PSPM operator will be multivalued in the
parameter
.According to this scheme it can be predicted for what
types of media the PSPM operator will be multivalued in the
parameter ![]() .
.