PSPM as a summation operator

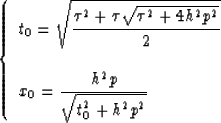
Spreading data along the DMO impulse response is identical with summing along a conjugate curve. For zero-offset migration in a constant velocity medium, spreading the data over circles produces the identical result with summing along hyperbolas. The DMO ellipse corresponds to the circle while the summation DMO-conjugate curve corresponds to the hyperbola. Each point along the summation curve contributes to the point situated on the top of the curve, just like summation is done along a hyperbola in zero-offset migration. The equations for the equivalent PSPM summation operator are

 

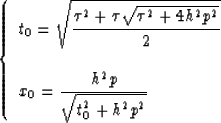$$\left \{ \begin{array} {l} t_0 = \displaystyle{ { \sqrt{ {\t... ...le{ { {h^2p \over \sqrt{t_0^2+h^2p^2} } }}\end{array} \right.$$ (4)

In Figure 2 the summation curves are represented in the same coordinates as the PSPM operator ($\tau$ and $\bf{p}$). The family of hyperbolic type curves corresponds to a constant $\tau$ parameter, while the vertical curves correspond to a constant $\bf{p}$ parameter. The cutoff is given by the same limits imposed on the parameter $\bf{p}$.

In Figure 3 is plotted the PSPM summation operator in order to correlate and compare it with the full prestack migration operator. For small velocities the PSPM operator and the full migration operator are identical. The full migration operator in the figure is limited laterally to the space between the source and receiver. The convergence of the full prestack summation curve to the PSPM operator for small velocities is easy to understand, as the migration ellipse for a medium with low velocity converges toward the PSPM ellipse, with semi-axis h.