Next: Solving for particle motions
Up: COUPLED WAVE PROPAGATION IN
Previous: Entropy Field Equation
Combining Equations 21,
23 and 25,
we end up with a coupled system of partial differential
equations.
In contrast to Equation 18, the wave equation corresponds to
the linear relationship between ``generalized stresses'' and ``generalized strains'', as given in Equation 7.
|  |
(26) |
However in this case, the spatial derivative operator in matrix form K
has to be in uncompacted notation
| 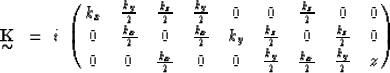 |
(27) |
in order to cast the problem in eigenvalue form
| 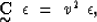 |
(28) |
which is the generalized Christoffel equation in elastic strain notation. The eigenvalues (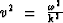 ) of this equation are again
propagation velocities of plane waves in the medium. The eigenvectors are
directly related to the particle motion. With this formulation,
in contrast to the displacement formulation,
we have to carry out an additional computational step in order to obtain
physically meaningful displacements, given the strains for a wave traveling in
a particular direction.
) of this equation are again
propagation velocities of plane waves in the medium. The eigenvectors are
directly related to the particle motion. With this formulation,
in contrast to the displacement formulation,
we have to carry out an additional computational step in order to obtain
physically meaningful displacements, given the strains for a wave traveling in
a particular direction.





Next: Solving for particle motions
Up: COUPLED WAVE PROPAGATION IN
Previous: Entropy Field Equation
Stanford Exploration Project
1/13/1998