




Next: Electromagnetic field equations
Up: WAVE EQUATIONS IN TERMS
Previous: WAVE EQUATIONS IN TERMS
The derivation of the coupled elastic wave equations is similar to that of the
uncoupled equations. In an elastic medium forces have to be in balance.
This implies that the divergence of the elastic stress tensor 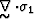 has to equal the product of mass density
has to equal the product of mass density 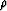 and the second temporal
derivative of the particle displacement
and the second temporal
derivative of the particle displacement  . We can also include a forcing
term
. We can also include a forcing
term 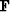 and get
and get
| 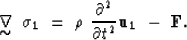 |
(5) |
The elastic strain 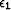 can be calculated by taking spatial derivatives
can be calculated by taking spatial derivatives
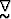 of the displacement
of the displacement  , as follows:
, as follows:
| 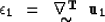 |
(6) |
Next we relate the components of the elastic stress 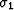 to the components
of the elastic strain
to the components
of the elastic strain 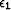 , the electric displacement
, the electric displacement 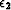 and the
first temporal derivative of the thermal displacement
and the
first temporal derivative of the thermal displacement
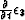 in the following equation:
in the following equation:
| 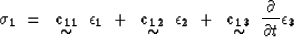 |
(7) |
Substituting Equation 7 into 5 gives a wave
equation in terms of elastic displacements (omitting the source term):
| 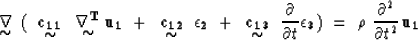 |
(8) |
This is a coupled wave equation for elastic displacements, since it includes
effects produced by electric and thermal displacements as well.





Next: Electromagnetic field equations
Up: WAVE EQUATIONS IN TERMS
Previous: WAVE EQUATIONS IN TERMS
Stanford Exploration Project
1/13/1998
![]() has to equal the product of mass density
has to equal the product of mass density ![]() and the second temporal
derivative of the particle displacement
and the second temporal
derivative of the particle displacement ![]() . We can also include a forcing
term
. We can also include a forcing
term ![]() and get
and get
![]() can be calculated by taking spatial derivatives
can be calculated by taking spatial derivatives
![]() of the displacement
of the displacement ![]() , as follows:
, as follows:
![]() to the components
of the elastic strain
to the components
of the elastic strain ![]() , the electric displacement
, the electric displacement ![]() and the
first temporal derivative of the thermal displacement
and the
first temporal derivative of the thermal displacement
![]() in the following equation:
in the following equation: