




Next: CHARACTERISTIC SURFACES
Up: Karrenbach: coupled wave propagation
Previous: Entropy field equations
Since Equations 8, 13
and 17 cannot be solved independently, we can, by combining
them, derive a coupled system of partial differential equations. In order to
investigate the nature of its solutions we can set up an analog to the
Christoffel equation (Auld, 1981) by looking
at plane wave solutions in a homogeneous medium. To do so, we
can Fourier transform the system of equations in space and time
(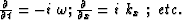 ). This operation results in an algebraic system of equations
for the unknown displacements
). This operation results in an algebraic system of equations
for the unknown displacements
|  |
(18) |
The spatial derivative operators in the form of matrices 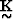 and
and 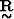 are
given in the Appendix.
Dividing Equation 18 by the square magnitude of the spatial
wave number vector
are
given in the Appendix.
Dividing Equation 18 by the square magnitude of the spatial
wave number vector 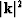 , we get the eigenvalue equation
, we get the eigenvalue equation
| 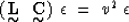 |
(19) |
which is the ``generalized'' Christoffel equation.
The eigenvalues (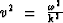 ) of this equation are
propagation velocities of plane waves in the medium. The eigenvectors are
directly related to the ``particle motions''.
Since
) of this equation are
propagation velocities of plane waves in the medium. The eigenvectors are
directly related to the ``particle motions''.
Since 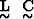 is dependent on direction cosines,
we can expect that propagation
velocity and particle motion are dependent on the propagation direction.
The dispersion relations become frequency dependent when we include heat
effects or if the medium is electrically conducting. At the zero frequency
limit, the contributions from heat and conductivity vanish.
This result is the same as if the medium were now purely piezoelectric.
is dependent on direction cosines,
we can expect that propagation
velocity and particle motion are dependent on the propagation direction.
The dispersion relations become frequency dependent when we include heat
effects or if the medium is electrically conducting. At the zero frequency
limit, the contributions from heat and conductivity vanish.
This result is the same as if the medium were now purely piezoelectric.





Next: CHARACTERISTIC SURFACES
Up: Karrenbach: coupled wave propagation
Previous: Entropy field equations
Stanford Exploration Project
1/13/1998

