Cross-coupled slowness surfaces

So far we have been looking at waves whose displacement type corresponds to their wave propagation speed. In these instances the waves propagate either at elastic speeds, exhibiting elastic particle motions, or at electromagnetic speeds, exhibiting electric displacements. Cross-coupled waves differ in their behaviour from those ``ordinary'' wavetypes: their particle motion is not congruent with their propagation velocity category. For such cross-coupled waves we get in general a much smaller particle motion magnitude compared with ``ordinary'' wavetypes. In Figure 5 slowness surfaces for waves traveling in quartz at elastic speeds are shown. The values of the speeds are the same as in Figure 4, however, this time electric particle motions are displayed. The general appearance resembles that of the purely elastic surfaces; the striking difference is that there is no purely longitudinal particle motion. All the particle motions have transverse components. Slowness surfaces of waves traveling in quartz at speeds comparable to that of electromagnetic waves maintain their shape. However the particle motions are not purely transversal any more, but also include longitudinal motions (introduced by coupling).

 

greenhornelastic
Figure 1 3D slowness surfaces for Greenhorn shale are calculated for wavetypes with elastic speeds using elastic constants. The material has transverse isotropic symmetry and is in appearance similar to that of PZT2.

 

AuldPZT2piezoel
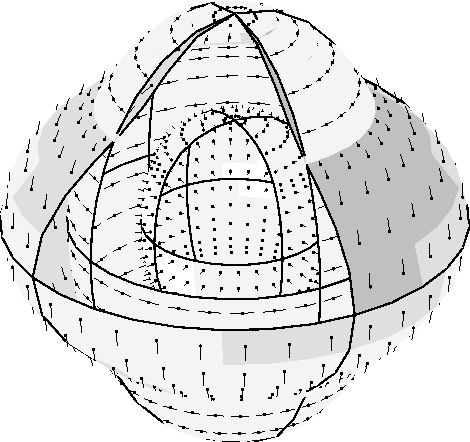
Figure 2 3D slowness surfaces for PZT2 are calculated for wavetypes with elastic speeds using elastic and piezoelectric constants. The material has transverse isotropic symmetry. The slowness along the vertical axis is greatly increased, due to piezoelectric coupling constants (see appendix). Mainly the slowest S-wave is affected and shown here.

 

AuldPZT2stiff
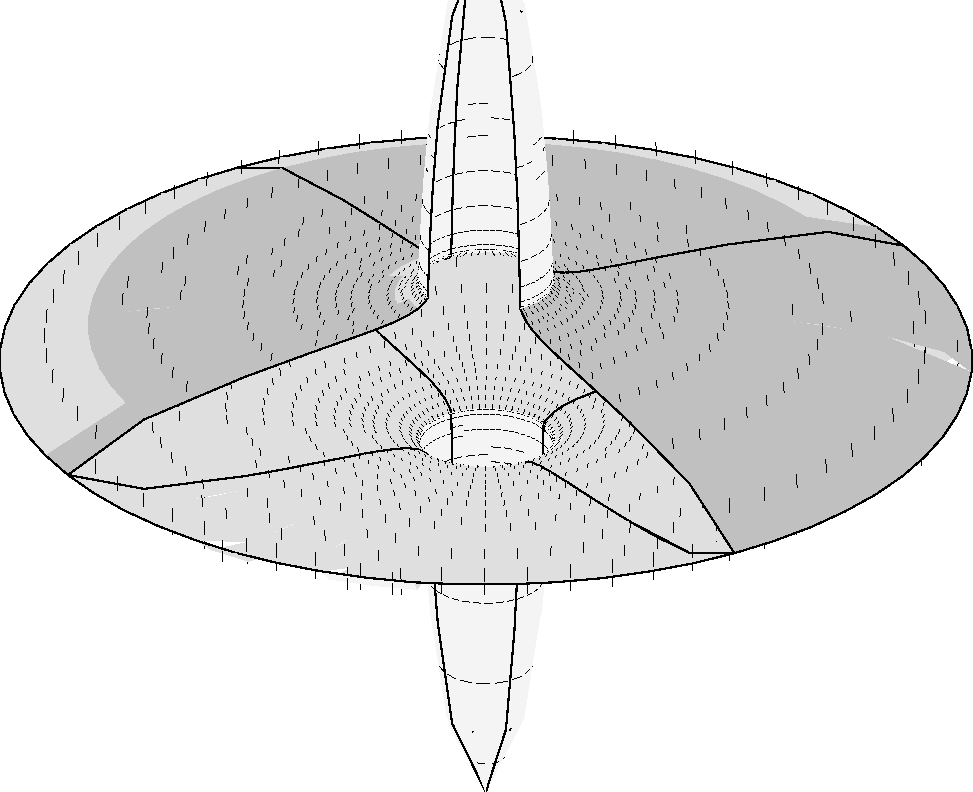
Figure 3 3D slowness surfaces for PZT2 are calculated for wavetypes with elastic speeds using elastic and piezoelectric constants. The material has transverse isotropic symmetry. The slowness along the vertical axis is still greatly increased, while additionally the slowness in the symmetry plane is increased to about the same magnitude, due to piezoelectric coupling and the influence of the boundary condition (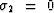$\sigma_2~=~0$). Mainly the slowest S-wave is affected and shown here.

 

AuldQUARTZpiezoel
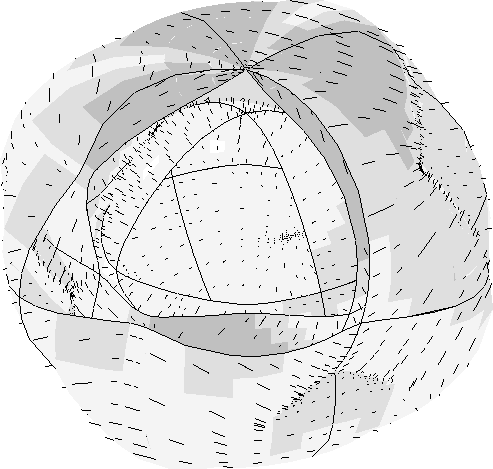
Figure 4 3D slowness surfaces for quartz are calculated for wavetypes with elastic speeds using elastic and piezoelectric constants. The material has hexagonal symmetry, which causes the two slowness surfaces for the s-waves to be of complicated shape. The difference between purely elastic and piezoelectric wave propagation is in the range of a couple percent deviation in slowness and particle motion.

 

AuldQUARTZpiezoelem
Figure 5 3D slowness surfaces for quartz are calculated for cross-coupled wavetypes with elastic speeds and electromagnetic particle motions, using elastic and piezoelectric constants. The material has hexagonal symmetry. The slowness surfaces for these waves are similar to those of ordinary elastic waves, but now show only purely transversal particle motion.