BOUNDARY CONDITIONS

In the description of the dynamic states of solid bodies, boundary conditions play a very important role from the theoretical as well as the experimental point of view. The dynamic state function can be reduced in the number of independent variables (degrees of freedom) by keeping specific variables fixed. This concept is intimately related to the principle of hidden variables in a dynamic system. Hidden variables do not appear explicitly in dynamic equations but are rather transformed into given boundary conditions. The simplest example is an elastic solid; its behavior differs, depending upon whether we specify an isothermal or an adiabatic boundary. Entropy and temperature do not appear explicitly in the constitutive equations, but rather in the statement that the temperature or entropy remains constant. The values of the elastic constants are different in both cases. Translating this notion into a more general formulation means that we keep some of either the generalized stresses or the generalized strains constant (or zero). By doing so, we specify two extremes of boundary conditions imposed on the wave propagation. Any other boundary condition can be generated from linear combinations of these two extremes. Consequently, since the description of a dynamic solid body is far from being completely specified by the three physical properties - elastic, electric, and thermal quantities - we can also include magnetic state variables. If we do not, however, we keep such variables implicitly constant.

In practice it seldom happens that we measure all state variables in one experiment. Thus we have to be aware of the effect that the implicit boundary conditions have on the realized values. Let me illustrate this effect using the PZT2 material. Figure shows pure elastic slowness surfaces. In this case we assume that the dynamic state is solely specified by the elastic constants, in other words, that all alien strains are kept at zero (boundary condition). In contrast, Figure shows the elastic slowness surfaces when we specify as a boundary condition that alien stresses (electrical field strength) are kept at zero. The difference in scale between the two figures is a factor of 4. In the latter case we acknowledge the existence of a hidden state variable and incorporate its effects in form of altered elastic constants. This phenomenon in piezoelectric material is commonly termed ``electrical stiffening''. 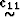The elastic constants $$\mathop{\mbox{${\bf c_{11}}$}}_{\mbox{$\sim$}}$$ are now modified to be $$\mathop{\mbox{${\bf c_{11}}$}}_{\mbox{$\sim$}} - \displaystyle \... ...}_{\mbox{$\sim$}} \displaystyle \mathop{\mbox{${\bf c_{21}}$}}_{\mbox{$\sim$}}$$.The shape of the two outermost slowness surfaces are altered significantly, while the innermost (p wave) does not change very much. However the intrinsic symmetry is the same in both cases. The comparison of the two extreme boundary conditions emphasizes the importance of including piezoelectrical effects, even when electromagnetic waves are not measured in an experiment.