Next: CONCLUSIONS
Up: IMAGES OF ARBITRARY REFLECTORS
Previous: Residual-moveout equation
Now we consider the image of a scatter in a homogeneous medium. Let the scatter have
coordinates (xt, zt). Then, the angle of incident ray to the vertical
is fixed.
| 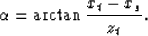 |
(13) |
The angle of the reflected ray can be any value between 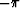 /2 and
/2 and
 /2. Therefore, equations (8) and (13) define
the image of the scatter in the migrated shot profile. Figure 6
shows the two examples of the image of a scatter.
We see that the image of the scatter is stretched out in both cases.
When
/2. Therefore, equations (8) and (13) define
the image of the scatter in the migrated shot profile. Figure 6
shows the two examples of the image of a scatter.
We see that the image of the scatter is stretched out in both cases.
When 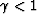 ,
the image moves upwards and curves downwards; when
,
the image moves upwards and curves downwards; when 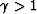 , the
image moves downwards and curves
upwards. Figure 6 also shows graphically that
the curves defined by equations (8) and (13) are indeed
the envelopes of migration ellipses.
envsca
, the
image moves downwards and curves
upwards. Figure 6 also shows graphically that
the curves defined by equations (8) and (13) are indeed
the envelopes of migration ellipses.
envsca
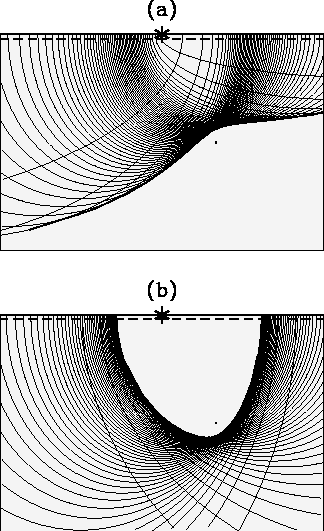
Figure 6 When the reflected energy from a scatter in a homogeneous
medium is migrated with a velocity
of (a) -10% error; (b) +10% error, the image of the scatter,
defined by the envelope of the
migration ellipses, is stretched out and (a) curves downwards; (b) curves
upwards.

For constant-velocity media, equations (8) and (13)
actually define the kinematics of the summation operator that does residual
migration for the migrated shot profiles. Figure 7 shows two sets
of curves computed from these two equations.
To revise distorted images on migrated shot
profiles, we can sum the data samples along the
curves defined by equations (8) and (13).
impres
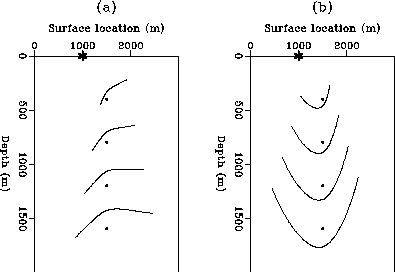
Figure 7 Examples of the kinematics of the summation operator that does residual
migration for the migrated shot profiles.
The star indicates the shot position.
The dots indicate the actual location of the scatters: (a) 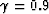 ;
(b)
;
(b) 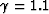 .
.






Next: CONCLUSIONS
Up: IMAGES OF ARBITRARY REFLECTORS
Previous: Residual-moveout equation
Stanford Exploration Project
1/13/1998