Next: Residual-moveout equation
Up: IMAGES OF ARBITRARY REFLECTORS
Previous: IMAGES OF ARBITRARY REFLECTORS
To understand how velocity errors influence the results of shot-profile
migration, we consider the simple case of a reflector of dipping angle
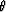 , located at (xt,zt) of a homogeneous medium of velocity vt.
As shown in Figure 2, a shot is at surface location xs
and a receiver is on the surface with coordinate x=xr.
We define
, located at (xt,zt) of a homogeneous medium of velocity vt.
As shown in Figure 2, a shot is at surface location xs
and a receiver is on the surface with coordinate x=xr.
We define  to be the angle of the incident
ray to the vertical and
to be the angle of the incident
ray to the vertical and 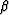 to be the angle of the reflected ray to the
vertical. Suppose we migrate shot records with velocity vm, and we want
to determine the location of the image of the reflector
on the migrated sections.
For a fixed shot location, the travel time
to be the angle of the reflected ray to the
vertical. Suppose we migrate shot records with velocity vm, and we want
to determine the location of the image of the reflector
on the migrated sections.
For a fixed shot location, the travel time 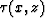 of
a reflection event is a function of the location of observation.
of
a reflection event is a function of the location of observation.
Now we apply Goldin's three-step method.
The first step is to find the travel time of the
reflection event observed by a receiver at x=xr on the earth's surface.
| 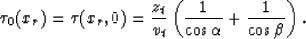 |
(1) |
where
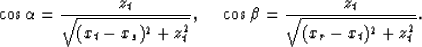
The next step is to find 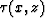 by solving Eiconal equation
by solving Eiconal equation
| 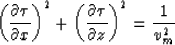 |
(2) |
with equation (1) as the boundary condition.
In a case of homogeneous media, the problem can be solved analytically.
| 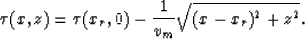 |
(3) |
It can be shown that (Goldin, 1982)
| 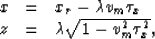 |
(4) |
where
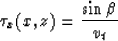
and 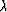 is a parameter to be determined.
is a parameter to be determined.
The last step is imaging. Let the travel time of the reflection event observed
at point (x,z) be equal to the travel time from the shot to this point.
| 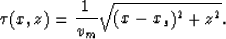 |
(5) |
Combining equations (1), (3) and (5), we
have relation
| 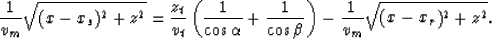 |
(6) |
To determine the 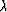 in equation (4), we replace x and
z in equation (6) with equation (4).
In Appendix A, I show that
in equation (4), we replace x and
z in equation (6) with equation (4).
In Appendix A, I show that
| ![\begin{displaymath}
\lambda ={z_t \over \gamma \cos \beta}[1+(\gamma^2-1)
{\cos^2 ({1 \over 2}(\beta -\alpha))
\over \cos \alpha \cos \beta }]\end{displaymath}](img15.gif) |
(7) |
and
| 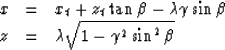 |
(8) |
where
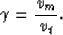
Thus, for given location (xt,zt) of a reflector
and the relationship between  and
and
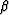 , we can compute the location (x,z) of the migrated image.
, we can compute the location (x,z) of the migrated image.
We consider, as an example, a plane reflector of dipping angle 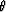 ,
,
| 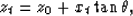 |
(9) |
that is illuminated by a shot at x=xs.
The relation between  and
and 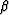 follows Snell's law,
follows Snell's law,
| 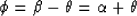 |
(10) |
where 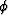 is the open angle between the incident (or reflected) ray and
the normal of the reflector.
Substituting this relation and equation (9) into
equations (7) and (8) offers us formulas
to compute the coordinates of the migrated image.
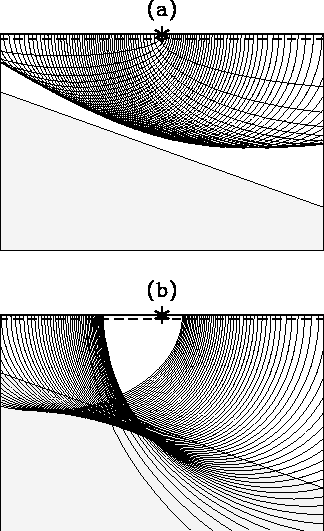
In Figure 3 are plotted the migrated images
for two different
is the open angle between the incident (or reflected) ray and
the normal of the reflector.
Substituting this relation and equation (9) into
equations (7) and (8) offers us formulas
to compute the coordinates of the migrated image.
In Figure 3 are plotted the migrated images
for two different 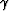 values.
When
values.
When 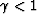 , the migrated image is stretched out and curves upwards;
when
, the migrated image is stretched out and curves upwards;
when 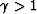 , the migrated image shrinks and curves downwards.
In Figure 3 is also drawn a set
of migration ellipses. As expected, the migrated images are the
envelopes of those migration ellipses.
envbed
, the migrated image shrinks and curves downwards.
In Figure 3 is also drawn a set
of migration ellipses. As expected, the migrated images are the
envelopes of those migration ellipses.
envbed
Figure 3 When the reflected energy from a plane reflector
in a homogeneous medium
is migrated with a velocity
of (a) -10% error; (b) +10% error, the image of the reflector,
defined by the envelope of the migration ellipses, is distorted from
the actual image of the reflector.
The dipping angle of the reflector is 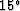 .
.






Next: Residual-moveout equation
Up: IMAGES OF ARBITRARY REFLECTORS
Previous: IMAGES OF ARBITRARY REFLECTORS
Stanford Exploration Project
1/13/1998
![]()
![]() by solving Eiconal equation
by solving Eiconal equation
![]()
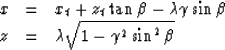
![]()
![]() ,
,