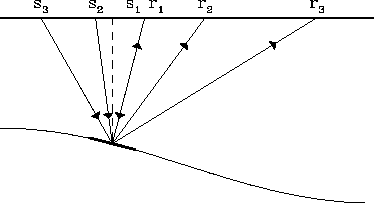
 |
Figure 1 In a multifold seismic experiment, a small portion of the subsurface is illuminated by shots at different offsets. The reflected energy is recorded by a receiver array on the surface.
In a multifold seismic experiment, a small portion of a subsurface is illuminated by shots at different offsets, as shown in Figure 1. The reflected energy is recorded by a receiver array on the surface. Imaging of such seismic reflection data can be accomplished by a prestack depth migration of individual shot records, followed by a stacking of the results at common surface locations. If the velocity model used for the shot-record migration does not correctly model the travel-times of reflection events, the images on migrated shot profiles at a constant surface location (CSL) will be distorted from one another. Under this circumstance, stacking of the CSL gathers can not effectively enchance the signal-noise ratio of the images. It may even damage the images.
 |
It is observed on field data that after profile migration, the moveout trajectories on CSL gathers can curve upwards or downwards, depending on the migration velocities being higher or lower than the true velocities. With these observations, Al-Yahya (Al-Yahya, 1989) employed profile migration for velocity analysis. In his method, velocity errors are estimated by measuring the curvatures of the residual moveout in CSL gathers. Al-Yahya's curvature scanning is based on the residual moveout (RMO) equation with common-midpoint (CMP) approximation.
It is noticed that when the velocities used in migration are not equal to the actual velocities of the media, the images of reflectors move away both horizontally and vertically from their actual position. Using asymptotic ray theory, Lemoine (Lemoine, 1989) extended Al-Yahya's method to the common-depth-point (CDP) concept. From second-order approximations, he derived an equation that relates velocity errors and measurable phase-contour curvatures.
Al-Yahya's work and Lemoine's work mentioned above have two common restrictions. First, the RMO equations they derived are approximations for small offset, large depth, and small velocity errors. Second, the equations assume horizontal reflectors. To attack the second restriction, both authors applied the residual-velocity analysis and shot-profile migration iteratively. However, such an iterative algorithm is expensive because residual-velocity estimation and shot-profile migration both are time-consuming.
Goldin (Goldin, 1982) proposed a three-step method to find the location of the image of a reflector on migrated sections. When a homogeneous medium is considered, this algorithm can give analytical solutions. As an example, Goldin derived a pair of parametric equations that describe the image of a horizontal reflector on a migrated shot profile.
In this paper, I apply Goldin's method for the purposes of residual-velocity analysis and residual migration. First, I extend Goldin's result to adapt arbitrary reflectors. Then, by specifying the relationship between the angles of the incident ray and the reflected ray, I find the residual-moveout equation for an arbitrary reflector and a residual-migration operator for a migrated shot-profile. I also use graphic tools to justify my solutions. In conclusion, I discuss the further work I want to investigate in the future.
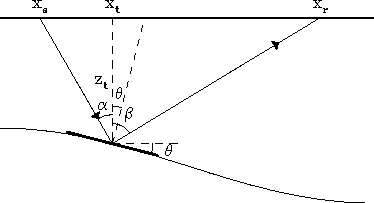 |