Without loss of generality, we consider experiments with a receiver array
spreading on the right side of the shot. (A split-spreading experiment can be
decomposed into two one-side spreading experiments). Let us first look
at a simple model that consists of a flat reflector with an overburden of
a constant velocity medium. We want to investigate how the image of the
reflector will be distorted as the parameter v in ![]() deviates
from the true velocity vt of the medium.
deviates
from the true velocity vt of the medium.
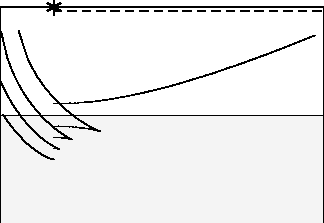
Goldin (1982) proved that when v is equal to ![]() the crossing
points of the caustics of rays and the image of the reflector are located
right below the shot location. In Figure 1, a sequence of
distorted images are drawn with
the crossing
points of the caustics of rays and the image of the reflector are located
right below the shot location. In Figure 1, a sequence of
distorted images are drawn with ![]() . We see that
when
. We see that
when ![]() , the image of the reflector is completely migrated
to the left side of the shot. Let us demonstrate this fact by graphics.
, the image of the reflector is completely migrated
to the left side of the shot. Let us demonstrate this fact by graphics.
 |
As I mentioned earlier, ![]() is a Kirchhoff migration
operator. Its output is the superposition of a set of migration ellipses.
Therefore the image I(t0,x) is constructed by the envelopes of these ellipses.
Because the principle axes of migration ellipses depend on the
parameter v, so do their envelopes.
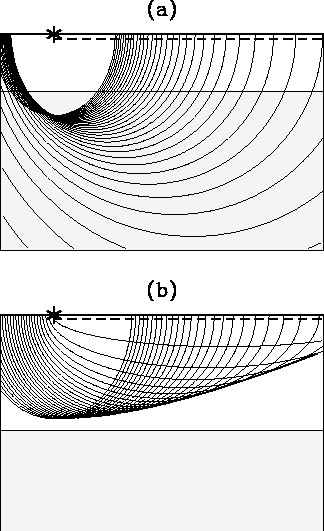
In Figure 2, I show a set of migration
ellipses and their envelopes. When
is a Kirchhoff migration
operator. Its output is the superposition of a set of migration ellipses.
Therefore the image I(t0,x) is constructed by the envelopes of these ellipses.
Because the principle axes of migration ellipses depend on the
parameter v, so do their envelopes.
In Figure 2, I show a set of migration
ellipses and their envelopes. When ![]() , the envelope of
the migration ellipses appears entirely on the left side of the shot. In contrast,
when v=0.9vt, the envelope of the migration ellipses appears entirely
on the right side of the shot.
In fact, it can be mathematically proved that, after the transformation
with operator
, the envelope of
the migration ellipses appears entirely on the left side of the shot. In contrast,
when v=0.9vt, the envelope of the migration ellipses appears entirely
on the right side of the shot.
In fact, it can be mathematically proved that, after the transformation
with operator ![]() , the images of the events whose velocities are
equal to
, the images of the events whose velocities are
equal to ![]() will be completely separable from the images of the
events whose velocities are greater than v.
will be completely separable from the images of the
events whose velocities are greater than v.
 |