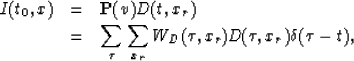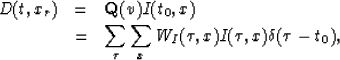Next: Choice of v
Up: PRINCIPLES OF THE ALGORITHM
Previous: Travel-time relations
Let D(t,xr) be a common shot gather (CSG). Define 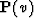 to be a velocity-dependent operator that transforms the data D(t,xr)
into its image I(t0,x).
to be a velocity-dependent operator that transforms the data D(t,xr)
into its image I(t0,x).
| 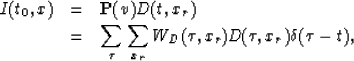 |
(3) |
| (4) |
where WD is a weighting function and t is defined in
equation (1). Notice that the operator 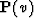 is actually
a Kirchhoff migration operator of constant velocity v. Similarly, the
backward transformation from I(t0,x) to D(t,xr) is
is actually
a Kirchhoff migration operator of constant velocity v. Similarly, the
backward transformation from I(t0,x) to D(t,xr) is
| 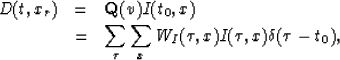 |
(5) |
| (6) |
where t0 is defined in equation (2). 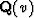 may be
the inverse or transpose of
may be
the inverse or transpose of 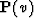 depending on the choice of
weighting function WI. The parameter v of the operators plays an
important role in both forward and backward transformations.
For the purpose of imaging, we
set v to be the velocity of the medium. As a result, I(t0,x)
will be the precise image of the earth. For other values of v, however,
I(t0,x) will be a distorted image. Our goal is to select a special
value of v such that after the forward transformation with operator
depending on the choice of
weighting function WI. The parameter v of the operators plays an
important role in both forward and backward transformations.
For the purpose of imaging, we
set v to be the velocity of the medium. As a result, I(t0,x)
will be the precise image of the earth. For other values of v, however,
I(t0,x) will be a distorted image. Our goal is to select a special
value of v such that after the forward transformation with operator
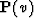 the images of the water bottom multiples are
as separable as possible from the images of other events.
the images of the water bottom multiples are
as separable as possible from the images of other events.





Next: Choice of v
Up: PRINCIPLES OF THE ALGORITHM
Previous: Travel-time relations
Stanford Exploration Project
1/13/1998
![]() to be a velocity-dependent operator that transforms the data D(t,xr)
into its image I(t0,x).
to be a velocity-dependent operator that transforms the data D(t,xr)
into its image I(t0,x).