




Next: Recursions: order updating
Up: THE LSL ALGORITHM
Previous: Forward residuals
We define the vectors of backward residuals rk,T-1 with the recursions:
| 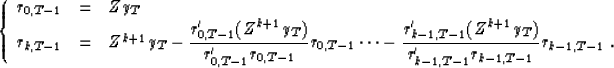 |
(1) |
The index 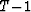 appears because these residuals can all be expressed as Z
applied to a known vector: r0,T=yT for example. These recursions
are in fact equivalent to performing a Gram-Schmidt orthogonalization
of the space
appears because these residuals can all be expressed as Z
applied to a known vector: r0,T=yT for example. These recursions
are in fact equivalent to performing a Gram-Schmidt orthogonalization
of the space 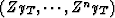 . Then, for any k, the space
. Then, for any k, the space
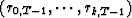 is equal to
is equal to 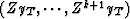 ; also,
rk,T-1 is orthogonal to
; also,
rk,T-1 is orthogonal to 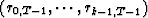 .So, with these recursions, we see that rk,T-1 is the orthogonal
complement of the shifted data Zk+1yT on
.So, with these recursions, we see that rk,T-1 is the orthogonal
complement of the shifted data Zk+1yT on 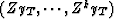 :
:

In other words, rk,T-1(t) is the residual obtained from the optimal
prediction of y(t-(k+1)) with the future values 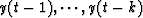 ;this explains the term ``backward'' residuals. The geometrical interpretations
of
;this explains the term ``backward'' residuals. The geometrical interpretations
of 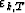 and rk,T-1 appear together on Figure
and rk,T-1 appear together on Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
Geometrical interpretation of the residuals 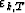 and
rk,T-1.
and
rk,T-1.
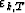 is the orthogonal complement of the data yT on Y1,k,T.
is the orthogonal complement of the data yT on Y1,k,T.
The predictable part of yT of order k is the orthogonal projection of yT on Y1,k,T.
rk,T-1 is the orthogonal complement of the shifted data Zk+1yT on Y1,k,T.
The new space of regressors Y1,k+1,T is 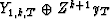 .
.
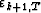 is the orthogonal complement of yT on Y1,k+1,T.
is the orthogonal complement of yT on Y1,k+1,T.
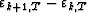 is equal to rk,T-1 multiplied by the reflection
coefficient Krk+1.
is equal to rk,T-1 multiplied by the reflection
coefficient Krk+1.
Finally, knowing that the forward residuals 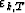 are the orthogonal
complement of yT on
are the orthogonal
complement of yT on 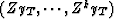 , so on
, so on
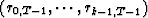 , we have the recursive formulas:
, we have the recursive formulas:





Next: Recursions: order updating
Up: THE LSL ALGORITHM
Previous: Forward residuals
Stanford Exploration Project
1/13/1998
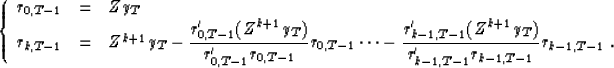
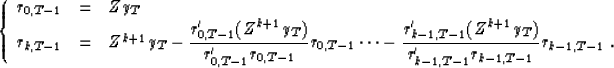
![]()
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
![]() and
rk,T-1.
and
rk,T-1.
![]() is the orthogonal complement of the data yT on Y1,k,T.
is the orthogonal complement of the data yT on Y1,k,T.
![]() .
. ![]() is the orthogonal complement of yT on Y1,k+1,T.
is the orthogonal complement of yT on Y1,k+1,T.
![]() is equal to rk,T-1 multiplied by the reflection
coefficient Krk+1.
is equal to rk,T-1 multiplied by the reflection
coefficient Krk+1.
![]() are the orthogonal
complement of yT on
are the orthogonal
complement of yT on ![]() , so on
, so on
![]() , we have the recursive formulas:
, we have the recursive formulas:
