




Next: Recursions: time updating
Up: THE LSL ALGORITHM
Previous: Backward residuals
Here, T is fixed, and the order of the prediction filter increases
from 1 to the desired order. The recursions implied for the backward residuals
need the weighting to be uniform (or exponential), essentially because
the recursions need a shift of these residuals; this condition is also
explained in Lee et al. (1981). These recursions are similar to those
of Burg's algorithm, and are directly derived from
equations (1) and (2):
| 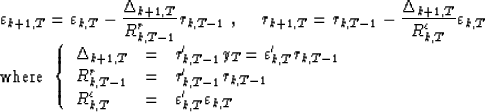 |
(2) |
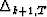 is called the partial correlation of the residuals;
Rrk,T-1 is the covariance of the backward residuals,
is called the partial correlation of the residuals;
Rrk,T-1 is the covariance of the backward residuals,
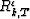 is the covariance of the forward residuals. Notice that
updating of the forward residuals has already been
illustrated by Figure
is the covariance of the forward residuals. Notice that
updating of the forward residuals has already been
illustrated by Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . We can also update these covariances
as follows:
. We can also update these covariances
as follows:
| 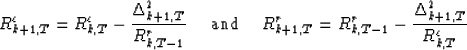 |
(3) |
Finally, we can define two reflection coefficients 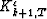 and
Krk+1,T, to give a compact expression of equation (
and
Krk+1,T, to give a compact expression of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ):
):
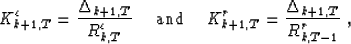
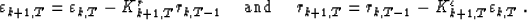
Notice also that we have two reflection coefficients. Burg's algorithm
only uses one coefficient. Normally, for an infinite stationary
sequence yT, these coefficients should be equal. However, in most practical
applications, this is not the case. Burg's algorithm corresponds in fact to a
particular choice of the reflection coefficient, which minimizes the total
energy 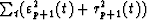 :
:
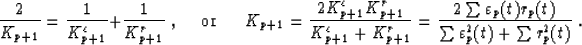
The advantage of Burg's algorithm is that the reflection coefficients Kp
are always bounded (by 1), preventing the algorithm from exploding numerically.
On the other hand, the backward residuals it uses don't provide us with
an orthogonal basis of the space of the regressors, and we cannot use
projection operators to solve the prediction problem.





Next: Recursions: time updating
Up: THE LSL ALGORITHM
Previous: Backward residuals
Stanford Exploration Project
1/13/1998
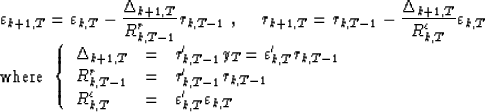
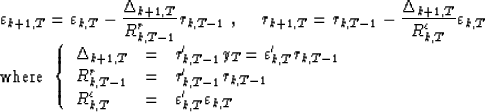
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . We can also update these covariances
as follows:
. We can also update these covariances
as follows:
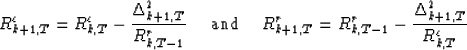
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ):
):
![]()
![]()
![]() :
:
![]()