




Next: Backward residuals
Up: THE LSL ALGORITHM
Previous: The basic LSL algorithm:
The forward residuals 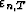 can be expressed in terms of orthogonal
projections. Effectively, defining
P1,n,T=A1,n,T(A'1,n,TA1,n,T)-1A'1,n,T, we have:
can be expressed in terms of orthogonal
projections. Effectively, defining
P1,n,T=A1,n,T(A'1,n,TA1,n,T)-1A'1,n,T, we have:
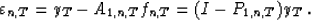
Because P21,n,T=P'1,n,T=P1,n,T, the operator P1,n,T is an
orthogonal projector. It projects the data vector yT on the space
Y1,n,T spanned by the columns of A1,n,T. These columns are simply
the past observations (or shifted data), ZyT to ZnyT, where Z
is the unit-delay shift operator.
The predictable part of yT is P1,n,TyT, the orthogonal
projection of yT on Y1,n,T. The residuals 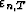 are then
orthogonal to this space: they are called the orthogonal complement
of yT on Y1,n,T. Their geometric interpretation is illustrated in
Figure
are then
orthogonal to this space: they are called the orthogonal complement
of yT on Y1,n,T. Their geometric interpretation is illustrated in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Defining the operator
.
Defining the operator 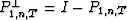 , the forward residuals
, the forward residuals
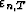 are
are 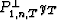 ;
; 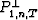 is also an
orthogonal projector.
is also an
orthogonal projector.
So, we need to compute P1,n,TyT. But this projection is easy to compute,
if we already know an orthogonal basis 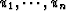 of the
space Y1,n,T. Effectively, the projection of yT is:
of the
space Y1,n,T. Effectively, the projection of yT is:
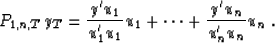
The backward residuals will in fact form this orthogonal basis.





Next: Backward residuals
Up: THE LSL ALGORITHM
Previous: The basic LSL algorithm:
Stanford Exploration Project
1/13/1998
![]()
![]() are then
orthogonal to this space: they are called the orthogonal complement
of yT on Y1,n,T. Their geometric interpretation is illustrated in
Figure
are then
orthogonal to this space: they are called the orthogonal complement
of yT on Y1,n,T. Their geometric interpretation is illustrated in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Defining the operator
.
Defining the operator ![]() , the forward residuals
, the forward residuals
![]() are
are ![]() ;
; ![]() is also an
orthogonal projector.
is also an
orthogonal projector.
![]() of the
space Y1,n,T. Effectively, the projection of yT is:
of the
space Y1,n,T. Effectively, the projection of yT is:
![]()