




Next: Forward residuals
Up: THE LSL ALGORITHM
Previous: THE LSL ALGORITHM
Suppose we want to predict a data sequence y(t) (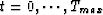 )from its own past values. The basic concept of the LSL algorithm is that,
to estimate the optimal residual at time T, we solve the prediction
problem in a least-squares sense on the window [0,T], and keep only the
residual at time T. To compute the residual at time
)from its own past values. The basic concept of the LSL algorithm is that,
to estimate the optimal residual at time T, we solve the prediction
problem in a least-squares sense on the window [0,T], and keep only the
residual at time T. To compute the residual at time 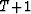 , we would
solve the problem on the window
, we would
solve the problem on the window ![$[0,T\!+\!1]$](img4.gif) , and again compute the residual
at time
, and again compute the residual
at time 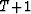 from that solution. This sequence explains why the final
residuals depend only on the past data.
from that solution. This sequence explains why the final
residuals depend only on the past data.
In mathematical formulation, we try to find n filter coefficients
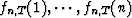 , minimizing:
, minimizing:
![\begin{displaymath}
\sum_{t=0}^T[\varepsilon_{n,T}(t)]^2 \mbox{\hspace{0.5cm}whe...
...cm}} \varepsilon_{n,T}(t)=y(t)-\sum_{i=1}^nf_{n,T}(i)y(t-i) \;.\end{displaymath}](img6.gif)
I define the data vectors yT, the residual vector 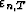 and
the convolution matrix A1,n,T:
and
the convolution matrix A1,n,T:
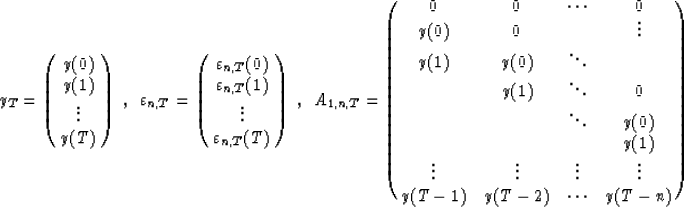
The prediction coefficients minimizing the residual energy are then equal to:
![\begin{displaymath}
f_{n,T}=[f_{n,T}(1),\cdots,f_{n,T}(n)]' = (A'_{1,n,T}A_{1,n,T})^{-1}A'_{1,n,T}y_T \;.\end{displaymath}](img9.gif)
We are solving a minimization problem on the data window [0,T], as indicated
by the subscript T. Especially, the filter coefficients fn,T depend
on T: if we work on the window ![$[0,T\!+\!1]$](img4.gif) , the least-squares solution
will be different, giving fn,T+1. The second subscript n means that we
are solving a problem for a filter of length n.
, the least-squares solution
will be different, giving fn,T+1. The second subscript n means that we
are solving a problem for a filter of length n.
In the classical approach, the final outputs are 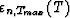 :we solve the problem on the whole window [0,Tmax]. In this case, the
final residuals also depend on the future data, because the filter coefficients
are computed with the whole set of data (
:we solve the problem on the whole window [0,Tmax]. In this case, the
final residuals also depend on the future data, because the filter coefficients
are computed with the whole set of data ( ). On the other
hand, the concept of the LSL algorithm is that the final outputs are the
residuals
). On the other
hand, the concept of the LSL algorithm is that the final outputs are the
residuals 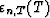 for all
for all 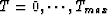 : this enables the
algorithm to adjust to variations in the statistics of the data.
: this enables the
algorithm to adjust to variations in the statistics of the data.
So, the LSL algorithm uses recursions for the residuals when we increase
the order n (order-updating), and the time T (time-updating). We can
also include exponential weighting, if we use a positive factor 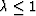 to minimize:
to minimize:
![\begin{displaymath}
\sum_{t=0}^T\lambda^{T-t}[\varepsilon_{n,T}(t)]^2 \ = \ \sum_{t=0}^T\lambda^{T-t}[y(t)-\sum_{i=1}^nf_{n,T}(i)y(t-i)]^2 \;.\end{displaymath}](img14.gif)
The matrix A'1,n,TA1,n,T would be the usual Toeplitz matrix involved
in the Wiener-Levinson algorithm, if we took only the data up to t=T-n
into account, but the form of A1,n,T is necessary for the time-update
recursions. This matrix A1,n,T will actually never be built, because
the aim of lattice methods is to work only with the residuals 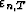 ,and not with the filter coefficients.
,and not with the filter coefficients.





Next: Forward residuals
Up: THE LSL ALGORITHM
Previous: THE LSL ALGORITHM
Stanford Exploration Project
1/13/1998
![]() , minimizing:
, minimizing:
![\begin{displaymath}
\sum_{t=0}^T[\varepsilon_{n,T}(t)]^2 \mbox{\hspace{0.5cm}whe...
...cm}} \varepsilon_{n,T}(t)=y(t)-\sum_{i=1}^nf_{n,T}(i)y(t-i) \;.\end{displaymath}](img6.gif)
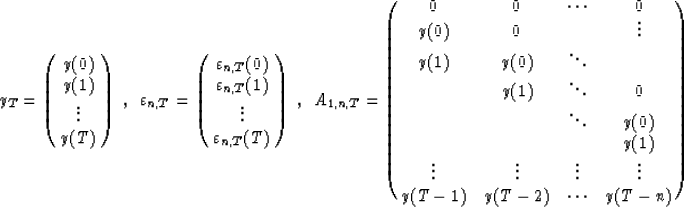
![]()
![]() :we solve the problem on the whole window [0,Tmax]. In this case, the
final residuals also depend on the future data, because the filter coefficients
are computed with the whole set of data (
:we solve the problem on the whole window [0,Tmax]. In this case, the
final residuals also depend on the future data, because the filter coefficients
are computed with the whole set of data (![]() ). On the other
hand, the concept of the LSL algorithm is that the final outputs are the
residuals
). On the other
hand, the concept of the LSL algorithm is that the final outputs are the
residuals ![]() for all
for all ![]() : this enables the
algorithm to adjust to variations in the statistics of the data.
: this enables the
algorithm to adjust to variations in the statistics of the data.
![]() to minimize:
to minimize:
![\begin{displaymath}
\sum_{t=0}^T\lambda^{T-t}[\varepsilon_{n,T}(t)]^2 \ = \ \sum_{t=0}^T\lambda^{T-t}[y(t)-\sum_{i=1}^nf_{n,T}(i)y(t-i)]^2 \;.\end{displaymath}](img14.gif)