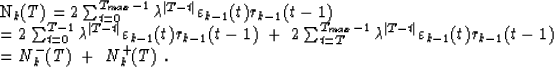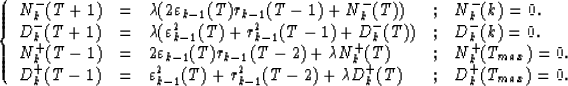Next: Is this algorithm rigorous?
Up: ADAPTIVE BURG-TYPE FILTERING
Previous: ADAPTIVE BURG-TYPE FILTERING
We still have a data sequence y(t) (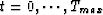 ).
For each time T and order k, we define the forward and backward residuals
).
For each time T and order k, we define the forward and backward residuals
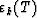 and rk(T); a single reflection coefficient
Kk and Burg's recursions are used:
and rk(T); a single reflection coefficient
Kk and Burg's recursions are used:
| 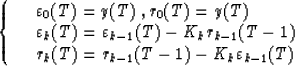 |
(9) |
To compute the reflection coefficients Kk, we minimize the weighted
energy of the forward and backward residuals of order k. The weights
are centered on the particular time T:
It is important to notice that the residuals depend here on the whole
set of data, since the energy 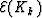 is a summation on the whole
time window. However, this expression of the energy induces an adaptive
formalism, since more emphasis is put on the residuals near the time T
of interest than of the residuals far from this time. Minimizing this
expression with respect to Kk leads to a time-dependent reflection
coefficient:
is a summation on the whole
time window. However, this expression of the energy induces an adaptive
formalism, since more emphasis is put on the residuals near the time T
of interest than of the residuals far from this time. Minimizing this
expression with respect to Kk leads to a time-dependent reflection
coefficient:
| 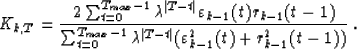 |
(10) |
Then Hale (1981) showed that the reflection coefficients Kk,T can be easily
computed, if the numerator and denominator of expression (11)
are split between past and future summations. For example, the numerator
becomes:
In the same way, we can split the denominator between D-k(T) (summation
up to 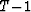 ), and D+k(T) (summation from T to Tmax).
Then, it is straightforward to show that:
), and D+k(T) (summation from T to Tmax).
Then, it is straightforward to show that:
| 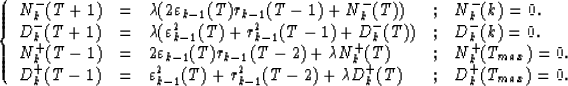 |
(11) |
These recursions, together with the recursions (10) and the
expression (11), form the adaptive version of Burg's algorithm.





Next: Is this algorithm rigorous?
Up: ADAPTIVE BURG-TYPE FILTERING
Previous: ADAPTIVE BURG-TYPE FILTERING
Stanford Exploration Project
1/13/1998
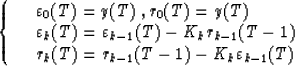
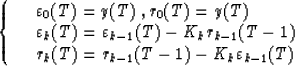
![]() is a summation on the whole
time window. However, this expression of the energy induces an adaptive
formalism, since more emphasis is put on the residuals near the time T
of interest than of the residuals far from this time. Minimizing this
expression with respect to Kk leads to a time-dependent reflection
coefficient:
is a summation on the whole
time window. However, this expression of the energy induces an adaptive
formalism, since more emphasis is put on the residuals near the time T
of interest than of the residuals far from this time. Minimizing this
expression with respect to Kk leads to a time-dependent reflection
coefficient: