First, to minimize the energy ![]() , we consider
that the same reflection coefficient is used for all the residuals at
different times; however, the minimization results in a time-dependent
coefficient. Second, the recursions (10) on the backward residuals
should be valid only when uniform or exponential weighting is used; here the
weights are pseudo-exponential (because they are symmetric), and the recursions
should not be valid. So, I have the impression that this
algorithm will effectively decrease the energy of the residuals,
but might as well not minimize it, because we don't give enough degrees
of freedom to let these residuals evolve from iteration to iteration.
, we consider
that the same reflection coefficient is used for all the residuals at
different times; however, the minimization results in a time-dependent
coefficient. Second, the recursions (10) on the backward residuals
should be valid only when uniform or exponential weighting is used; here the
weights are pseudo-exponential (because they are symmetric), and the recursions
should not be valid. So, I have the impression that this
algorithm will effectively decrease the energy of the residuals,
but might as well not minimize it, because we don't give enough degrees
of freedom to let these residuals evolve from iteration to iteration.
I have tried to use the same formalism as for the LSL algorithm, but I
could not find any logical relation between the two algorithms. The ideal
would be to use again the residuals ![]() and rk,T(t),
where the subscript T reappears, because we want to minimize the energy:
and rk,T(t),
where the subscript T reappears, because we want to minimize the energy:
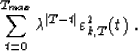

However, some problems appear in the order-updating recursions. First,
as I said, the updating of the backward residuals is not rigorous:
it implies a shift of these residuals, and we need an orthogonality condition
to be preserved even after this shift. This is not true with the weights
of Burg's adaptive algorithm. This problem had already been approached
by Claerbout (1977), who derived a Burg-type algorithm for weighted prediction
problems. However, Claerbout recognized that he didn't know exactly what
this algorithm was solving. I tried it on a simple numerical problem, and
I found an error of ![]() between the exact solution and the solution
of the algorithm, which confirms that the solution of an arbitrary weighted
problem cannot be reached with a totally recursive algorithm.
between the exact solution and the solution
of the algorithm, which confirms that the solution of an arbitrary weighted
problem cannot be reached with a totally recursive algorithm.
Moreover, the recursions in Hale's algorithm involve
the values rk-1,T-1(t)
(![]() ) to compute
the reflection coefficient Krk,T, while the recursion (11)
uses the values rk-1,t-1(t) (for all t).
) to compute
the reflection coefficient Krk,T, while the recursion (11)
uses the values rk-1,t-1(t) (for all t).
So, I must concede that I could not derive any mathematical formulation of Hale's algorithm comparable to the LSL algorithm. That lack of formulation makes me say that Burg's adaptive algorithm is rather intuitive.
To conclude this part, I recognize that this algorithm, exact for
![]() , is a good approximation of the ideal solution (which may
not be recursive) for
, is a good approximation of the ideal solution (which may
not be recursive) for ![]() close to 1. Effectively, some theoretical
obstacles disappear for such values of
close to 1. Effectively, some theoretical
obstacles disappear for such values of ![]() . First, in the minimization
of
. First, in the minimization
of ![]() , we can at first hand consider that Kk is the same for
all times t, even if it results in a time-varying expression: the reflection
coefficient will actually be slowly varying. Then, when deriving the
recursions, the weighting will be uniform on a large scale of time, which
makes Burg-type recursions more plausible.
, we can at first hand consider that Kk is the same for
all times t, even if it results in a time-varying expression: the reflection
coefficient will actually be slowly varying. Then, when deriving the
recursions, the weighting will be uniform on a large scale of time, which
makes Burg-type recursions more plausible.
So, even if this algorithm
does not exactly minimize the residuals, it will give a good approximation
of the residuals. Actually, Hale himself noticed in his paper (1981) that
it was necessary to keep ![]() close to 1.
close to 1.