




Next: SAMPLING IN VELOCITY DOMAIN
Up: DATA INVERSION
Previous: Modifications of basic equations
In Appendix A transpose operators to hyperbola and parabola stacking in
continuous domain are derived.
For hyperbola stacking 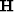 it is
weighted parabola stacking in
it is
weighted parabola stacking in 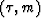 -space, which is symbolically
denoted as
-space, which is symbolically
denoted as 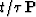 , and for parabola stacking
, and for parabola stacking 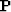 in
in
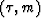 -space it is weighted stacking
-space it is weighted stacking 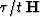 in (t,x)-space.
A dot product test was used to test these results (Table 1).
The following form of the
dot product test was used:
in (t,x)-space.
A dot product test was used to test these results (Table 1).
The following form of the
dot product test was used:
| 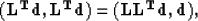 |
(13) |
where 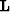 is
is 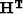 ,
, 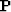 or whatever operator was used.
or whatever operator was used.
Table 1:
Dot product test for
various operators.
| 2|c|Operator in |
2|c|Dot product |
|
|
| time domain |
sloth domain |
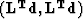 |
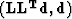 |
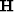 |
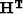 |
110.5207 |
110.5218 |
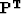 |
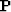 |
106.6519 |
106.6530 |
|---|
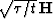 |
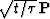 |
107.6680 |
108.4489 |
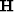 |
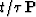 |
110.5207 |
111.3971 |
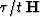 |
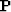 |
105.1228 |
105.8237 |
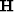 |
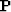 |
110.5207 |
108.4480 |
From the table we can see that adjoint operators derived in the continuous
domain are much less precise (relative error about 0.7-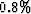 ) than adjoint operators derived in the
discrete domain (relative error
) than adjoint operators derived in the
discrete domain (relative error 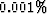 ).
Operators
).
Operators 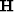 and
and 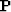 in the last line of the table are not
adjoint to each other, but they were tested to support the theoretical
results from Appendix A (relative error about
in the last line of the table are not
adjoint to each other, but they were tested to support the theoretical
results from Appendix A (relative error about 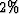 ).
).





Next: SAMPLING IN VELOCITY DOMAIN
Up: DATA INVERSION
Previous: Modifications of basic equations
Stanford Exploration Project
1/13/1998
![]() ) than adjoint operators derived in the
discrete domain (relative error
) than adjoint operators derived in the
discrete domain (relative error ![]() ).
Operators
).
Operators ![]() and
and ![]() in the last line of the table are not
adjoint to each other, but they were tested to support the theoretical
results from Appendix A (relative error about
in the last line of the table are not
adjoint to each other, but they were tested to support the theoretical
results from Appendix A (relative error about ![]() ).
).