Although sophisticated higher-order finite-difference schemes exist for the solution of the flux-conservative equation (Centrella and Wilson, 1984; Hawley et al., 1984), a first-order upwind finite-difference scheme is generally accurate enough for geophysical applications. I implemented a first-order method described by Engquist and Osher (1980).
Depending on the flow direction, upwind finite-difference schemes use a backward or forward finite-difference approximation to the derivative operator. The idea is that, although centered approximations are mathematically more accurate, the underlying physics may dictate otherwise. In other words, it is better to make a big error that is not transported, than to make a small one that blows up. The first-order forward and backward finite differences in space are, respectively:
| (5) |
Using the above finite-difference scheme, equation (3) is approximated by:
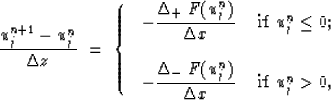 |
(6) |
Engquist and Osher solve the unstability problem in the shock region with the following scheme:
| (7) |
| |
(8) |