Flux-conservative equation

Similar to the conversion of the full wave equation into a one-way wave equation, we can rewrite the eikonal equation as a one-way equation that can be solved with standard techniques.

First, use 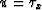$\u = \t_x$ to rewrite equation (1) as  

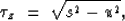$$\t_z\ =\ \sqrt{s^2 - \u^2},$$ (2)

By choosing a positive sign in front of the square root, and by using 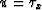$\u = \t_x$ instead of 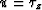$\u=\t_z$ as the substitution variable, we limit ourselves to downward-traveling rays. I will come back to these choices in one of the later sections.

Second, take the derivative of this equation with respect to x:  

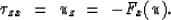$$\t_{zx}\ =\ \u_z\ =\ -F_x(\u).$$ (3)

where the function 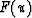$F(\u)$ is defined as

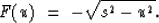$$F(\u) \ =\ -\sqrt{s^2 - \u^2}.$$ (4)

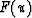$F(\u)$ is called the conserved flux; if 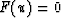$F(\u) = 0$, the rays do not ``flow'' downward anymore, but travel horizontally.

The (one-way) eikonal equation now has the form of a flux-conservative equation This is a well-known equation in computational fluid dynamics, and it can be solved in many ways (for example, see Roache, 1976). The next section discusses one particular solution.