A new bidirectional deconvolution method that overcomes the minimum phase assumption

Inverting a 2D synthetic section

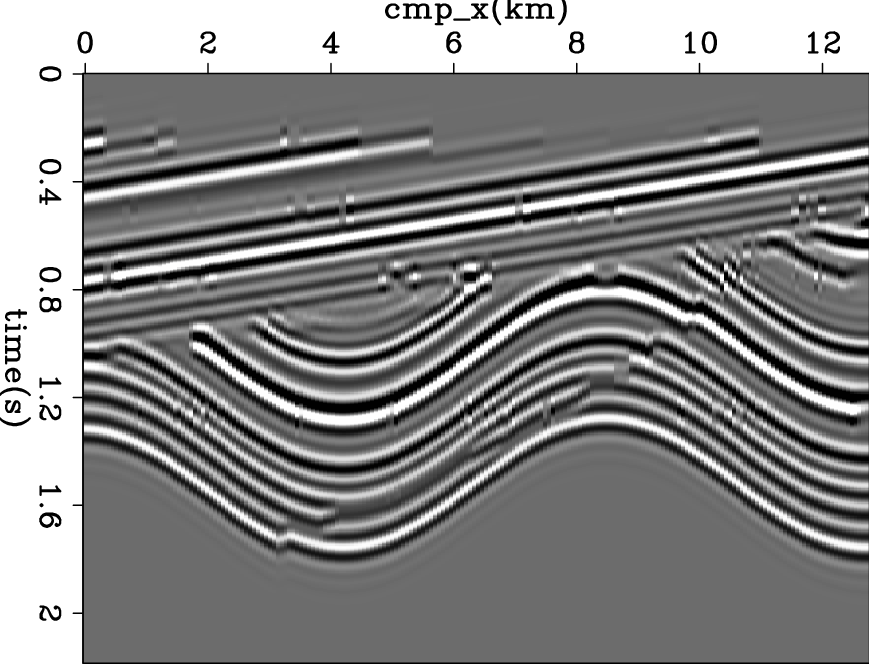
As in the previous report (Zhang and Claerbout, 2010), we use a 2D synthetic reflectivity model from Claerbout (2009b). Figure 5(a) shows the starting reflectivity model. Figure 5(b) shows the data generated by convolving the reflectivity model with wavelet 3. All traces use the same wavelet when generating the data, and all traces share the same wavelet when we are doing the deconvolution.

Previously the traditional sparse deconvolution failed on this example because of the symmetric wavelet; therefore, here we compare the old method and the bidirectional deconvolution method. Figure 6(a) shows the result using the old method (equation (3)). Figure 6(b) shows the result using the bidrectional deconvolution method (equation (4)). Comparing to the given model, the bidirectional deconvolution result is a spectacular improvement over the old one. Bidirectional deconvolution is a big improvement.

refl-jon,data-syn-sym-2d
Figure 5. (a) The 2D synthetic reflectivity model; (b) the synthetic data generated using wavelet 3.

mod-sym-2d-old,mod-sym-2d
Figure 6. (a) reflectivity model retrieved from the original method; (b) reflectivity model retrieved from the bidirectional deconvolution method.

A new bidirectional deconvolution method that overcomes the minimum phase assumption