 |
 |
 |
 | A new bidirectional deconvolution method that overcomes the minimum phase assumption |  |
![[pdf]](icons/pdf.png) |
Next: Data Examples
Up: Zhang and Claerbout: Hybrid
Previous: Zhang and Claerbout: Hybrid
In the previous report (Zhang and Claerbout, 2010), we introduced the spiking
deconvolution problem using the hybrid norm solver
(Claerbout, 2009a). Synthetic examples (Zhang and Claerbout, 2010)
showed that given a minimum-phase wavelet, it retrieved the sparse
reflectivity model almost perfectly even with a reflection series that is
far from white, while conventional L2
deconvolution did a poor job. However, if the assumption of a
minimum-phase wavelet was removed, the hybrid norm spiking deconvolution
failed quickly and gave a poor result similar to the conventional L2
deconvolution.
In this paper, we still rely on the hybrid norm solver to retrieve the
sparse model, but we use a slightly more complex formulation that
avoids the minimum-phase wavelet constraint.
We start by realizing that any (mixed-phase) wavelet 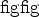 can be
decomposed into a minimum-phase part
can be
decomposed into a minimum-phase part 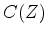 and a maximum-phase part
and a maximum-phase part
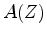 plus a certain time shift:
plus a certain time shift:
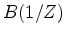 |
(1) |
where 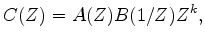 is also a minimum-phase wavelet (therefore
is also a minimum-phase wavelet (therefore 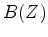 is
a maximum-phase wavelet) and the exponent
is
a maximum-phase wavelet) and the exponent 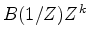 is the order of
is the order of 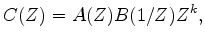 . This
. This
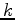 term makes the wavelet
term makes the wavelet 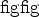 causal. In the time domain,
(1) can be written as
causal. In the time domain,
(1) can be written as
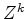 |
(2) |
where 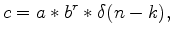 stands for the time reverse of series
stands for the time reverse of series 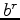 .
.
Our original spiking deconvolution can find only a minimum-phase wavelet which
has the same spectrum of real wavelet 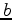 . It can be defined as an inverse
problem as follows:
. It can be defined as an inverse
problem as follows:
![$\displaystyle [d]f_c = r,$](img16.png) |
(3) |
where ![$ [d]$](img17.png) is the data convolution operator, and
is the data convolution operator, and 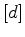 is the
unknown filter. In this formulation, the filter is the only unknown,
the hybrid norm is applied on the residual term
is the
unknown filter. In this formulation, the filter is the only unknown,
the hybrid norm is applied on the residual term 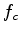 to enforce the
sparseness constraint. In theory, the residual
to enforce the
sparseness constraint. In theory, the residual 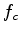 itself is the
reflectivity model. Such a method requires the wavelet in the data
to be minimum-phase because only a minimum-phase wavelet has a
causal stable inverse.
itself is the
reflectivity model. Such a method requires the wavelet in the data
to be minimum-phase because only a minimum-phase wavelet has a
causal stable inverse.
The following bidirectional deconvolution formulation utilizes a pair of conventional
deconvolutions, trying to invert components 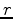 and
and 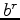 separately:
separately:
![\begin{displaymath}\begin{array}{l} \left[(d*f_b^r) \right] f_a = r_{a}, \\ \left[(d*f_a)^r \right] f_b = r_{b}, \end{array}\end{displaymath}](img21.png) |
(4) |
in which 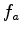 and
and 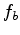 are the corresponding filters that corresponds to the
inverses of
are the corresponding filters that corresponds to the
inverses of 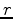 and
and 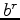 denoted above, the superscript
denoted above, the superscript 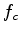 means
time-reverse. The operator in each equation is the convolution
operator. Again the hybrid norm is applied to
means
time-reverse. The operator in each equation is the convolution
operator. Again the hybrid norm is applied to  and
and 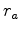 , and the
reflectivity model is simply
, and the
reflectivity model is simply 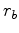 plus a time shift. Notice that
this is a non-linear inversion, since the operator itself depends on
the unknown
plus a time shift. Notice that
this is a non-linear inversion, since the operator itself depends on
the unknown 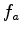 and
and 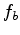 . In practice we have to solve these two
inversions alternately and therefore iteratively.
. In practice we have to solve these two
inversions alternately and therefore iteratively.
To understand the meaning of (4), let
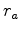 |
(5) |
where m is the reflectivity model and the 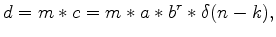 term is just a
time shift. Assume
term is just a
time shift. Assume 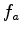 and
and 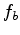 are perfectly known in the
operators (which is not true in reality), i.e.
are perfectly known in the
operators (which is not true in reality), i.e.
Substituting (5) into (4), since
we have
![\begin{displaymath}\begin{array}{l} \left[(m*\delta(n-k))*a \right] f_a = r_{a}, \\ \left[(m^r*\delta(n+k))*b \right] f_b = r_{b}. \end{array}\end{displaymath}](img33.png) |
(8) |
From (8) it is easier to see what is behind the bidirectional deconvolution
formulation (4): It tries to separate the two parts of the
wavelet, turning each one into a traditional deconvolution problem
in which the wavelet (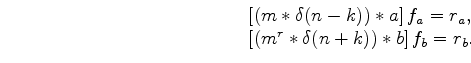 ) is always minimum-phase.
) is always minimum-phase.
As with all non-linear estimation, iteration is required. Convergence is assured
if the starting solution is close enough. We expect the traditional PEF for 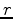 and an
impulse function for
and an
impulse function for 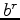 to be a pretty good first guess. The following section shows
several examples (complexity varies from low to high) illustrating the effectiveness
and limitations of the method.
to be a pretty good first guess. The following section shows
several examples (complexity varies from low to high) illustrating the effectiveness
and limitations of the method.
 |
 |
 |
 | A new bidirectional deconvolution method that overcomes the minimum phase assumption |  |
![[pdf]](icons/pdf.png) |
Next: Data Examples
Up: Zhang and Claerbout: Hybrid
Previous: Zhang and Claerbout: Hybrid
2010-11-26
![]() can be
decomposed into a minimum-phase part
can be
decomposed into a minimum-phase part ![]() and a maximum-phase part
and a maximum-phase part
![]() plus a certain time shift:
plus a certain time shift:
![]() . It can be defined as an inverse
problem as follows:
. It can be defined as an inverse
problem as follows:
![]() and
and ![]() separately:
separately:
 and
and 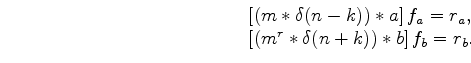 ) is always minimum-phase.
) is always minimum-phase.
![]() and an
impulse function for
and an
impulse function for ![]() to be a pretty good first guess. The following section shows
several examples (complexity varies from low to high) illustrating the effectiveness
and limitations of the method.
to be a pretty good first guess. The following section shows
several examples (complexity varies from low to high) illustrating the effectiveness
and limitations of the method.