In optimization problems, the
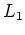
norm outperforms the
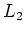
norm in presence of noise and when a blocky or sparse solution is appropriate.
These applications call for a solver that can redefine the optimum criteria for a particular problem.
We have implemented a generalized norm solver that is useful for a wide range of problems. Our solver modularizes the norm function so that it can easily be interchanged to experiment with different schemes on any particular geophysical problem. We implement
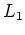
,
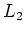
, and two additional norms: Huber and Hybrid
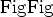
. These are useful for problems that seek the benefits of both the
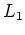
and
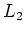
norms.