|
|
|
|
Generalized-norm conjugate direction solver |
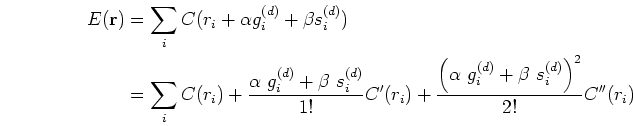 is the residual from the current iteration. The Taylor series expansion in Equation 8 lets us find analytical derivatives of the misfit function
is the residual from the current iteration. The Taylor series expansion in Equation 8 lets us find analytical derivatives of the misfit function
| (17) | |||
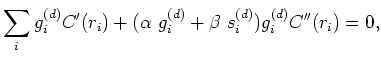 |
(18) |
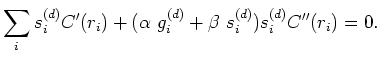 |
(19) |
|
|
|
|
Generalized-norm conjugate direction solver |